题目内容
【题目】如图,已知在△ABC中,AB=AC,tan∠B=2,BC=4,D为BC边的中点,点E在BC边的延长线上,且CE=BC,连接AE,F为线段AE的中点 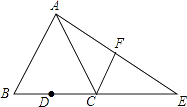
(1)求线段CF的长;
(2)求∠CAE的正弦值.
【答案】
(1)解:如图,连接AD,
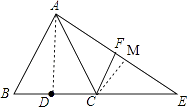
∵AB=AC,且D为BC中点,BC=4,
∴AD⊥BC,BD=CD=2,
∵tanB= ![]() =2,
=2,
∴AD=BDtanB=4,
∴AB=AC= ![]() =
= ![]() =2
=2 ![]() ,
,
又∵BC=CE,AF=EF,
∴CF= ![]() AB=
AB= ![]()
(2)解:如图,过点C作CM⊥AE于点M,
∴∠AMC=∠EMC=90°,
在Rt△ADE中,由勾股定理可得:AE= ![]() =
= ![]() =2
=2 ![]() ,
,
∵由勾股定理得;CM2=AC2﹣AM2=CE2﹣EM2,
∴(2 ![]() )2﹣AM2=42﹣(2
)2﹣AM2=42﹣(2 ![]() ﹣AM)2,
﹣AM)2,
解得:AM= ![]() ,
,
CM= ![]() =
= ![]() =
= ![]() ,
,
∴∠CAE的正弦值是 ![]() =
= ![]() =
= ![]()
【解析】(1)连接AD,由等腰三角形三线合一性质可得AD⊥BC,BD=CD=2,根据tanB= ![]() =2可得AD=4,由勾股定理得AB=AC=2
=2可得AD=4,由勾股定理得AB=AC=2 ![]() ,根据BC=CE、AF=EF即可得CF=
,根据BC=CE、AF=EF即可得CF= ![]() AB.(2)过C作CM⊥AE于M,则∠CMA=∠CME=90°,在Rt△ADE中,由勾股定理求出AE,由勾股定理得出方程(2
AB.(2)过C作CM⊥AE于M,则∠CMA=∠CME=90°,在Rt△ADE中,由勾股定理求出AE,由勾股定理得出方程(2 ![]() )2﹣AM2=42﹣(2
)2﹣AM2=42﹣(2 ![]() ﹣AM)2 , 求出AM,求出CM,即可求出答案.
﹣AM)2 , 求出AM,求出CM,即可求出答案.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.

 阅读快车系列答案
阅读快车系列答案【题目】某小学三年级到六年级的全体学生参加“礼仪”知识测试,试题共有10题,每题10分.从中随机抽取了部分学生的成绩进行统计,发现抽测的学生每人至少答对了6题,现将有关数据整理后绘制成如下“年级人数统计图”和尚未全部完成的“成绩情况统计表”.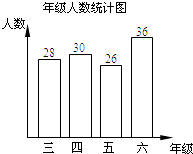
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
根据图表中提供的信息,回答下列问题:
(1)请将统计表补充完整
成绩情况统计表
成绩 | 100分 | 90分 | 80分 | 70分 | 60分 |
人数 | 21 | 40 | 5 | ||
频率 | 0.3 |
(2)测试学生中,成绩为80分的学生人数有 名;众数是 分;中位数是 分;
(3)若该小学三年级到六年级共有1800名学生,则可估计出成绩为70分的学生人数约有 名.