Question

【题目】如图，已知△ABC中，AB=AC=3，BC=2，点D是边AB上的动点，过点D作DE∥BC，交边AC于点E，点Q是线段DE上的点，且QE=2DQ，连接BQ并延长，交边AC于点P．设BD=x，AP=y．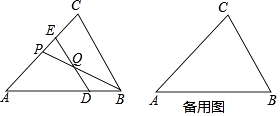
（1）求y关于x的函数解析式及定义域；
（2）当△PQE是等腰三角形时，求BD的长；
（3）连接CQ，当∠CQB和∠CBD互补时，求x的值．

Answer 1

【答案】
（1）解：如图所示，

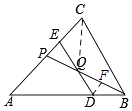
过点D作DF∥AC，交BP于F，则

根据QE=2DQ，可得

= ，

又∵DE∥BC，

∴ =1，

∴EC=BD=x，PE=3﹣x﹣y，DF= ，

∵DF∥AC，

∴ ，即 = ，

∴y= ，定义域为：0＜x＜3；

（2）解：∵DE∥BC，

∴△PEQ∽△PBC，

∴当△PEQ为等腰三角形时，△PBC也为等腰三角形，

①当PB=BC时，△ABC∽△BPC，

∴BC2=CPAC，即4=3（3﹣y），

解得y= ，

∴ = ，

解得x= =BD；

②当PC=BC=2时，AP=y=1，

∴ =1，

解得x= =BD；

③当PC=PB时，点P与点A重合，不合题意；

（3）解：∵DE∥BC，

∴∠BDQ+∠CBD=180°，

又∵∠CQB和∠CBD互补，

∴∠CQB+∠CBD=180°，

∴∠CQB=∠BDQ，

∵BD=CE，

∴四边形BCED是等腰梯形，

∴∠BDE=∠CED，

∴∠CQB=∠CED，

又∵∠DQB+∠CQB=∠ECQ+∠CED，

∴∠DQB=∠ECQ，

∴△BDQ∽△QEC，

∴ ，即2DQ2=x2，

∴DQ= ，DE= ，

∵DE∥BC，

∴ ，即 = ，

解得x= ．

【解析】（1）过点D作DF∥AC，交BP于F，根据平行线分线段成比例定理，可得EC=BD=x，PE=3﹣x﹣y，DF= ，进而根据DF∥AC，求得y= ，定义域为：0＜x＜3；（2）当△PEQ为等腰三角形时，△PBC也为等腰三角形，分三种情况讨论：①当PB=BC时，②当PC=BC=2时，③当PC=PB时，分别求得BD的长即可；（3）先根据已知条件判定四边形BCED是等腰梯形，判定△BDQ∽△QEC，得出 ，即2DQ2=x2 ， 再根据DE∥BC，得出 ，即 = ，求得x的值即可．
【考点精析】掌握等腰梯形的性质和平行线分线段成比例是解答本题的根本，需要知道等腰梯形的两腰相等；同一底上的两个角相等；两条对角线相等；三条平行线截两条直线，所得的对应线段成比例．