题目内容
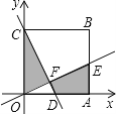
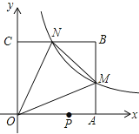
【题目】如图,在平面直角坐标系中,反比例函数![]() 的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
的图象与边长是6的正方形OABC的两边AB、BC分别相交于M、N两点,△OMA的面积为6.
(1)求反比例函数![]() 的解析式;
的解析式;
(2)若动点P在x轴上,求PM+PN的最小值.
【答案】(1)y=![]() ;(2)4
;(2)4![]()
【解析】
(1)由正方形OABC的边长是6,得到点M的横坐标和点N的纵坐标为6,求得M(6,![]() ),根据三角形的面积求得k的值;
),根据三角形的面积求得k的值;
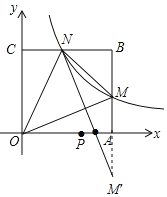
(2)作M关于x轴的对称点M′,连接NM′交x轴于P,则NM′的长=PM+PN的最小值,根据勾股定理即可得到结论.
解:(1)∵正方形OABC的边长是6,
∴点M的横坐标和点N的纵坐标为6,
∴M(6,![]() ),N(
),N(![]() ,6),
,6),
∵△OMA的面积为6,
∴![]() ×6×
×6×![]() =6,
=6,
∴k=12,
∴反比例函数y=![]() (x>0,k≠0)的解析式为y=
(x>0,k≠0)的解析式为y=![]() ;
;
(2)由y=![]() 可得M(6,2)和N(2,6),作M关于x轴的对称点M′,
可得M(6,2)和N(2,6),作M关于x轴的对称点M′,
∴AM=AM′=2,连接NM′交x轴于P,则M′N的长等于PM+PN的值最小,
∵AB=6,
∴BM′=8,BN=4,根据勾股定理求得NM′=![]() =4
=4![]() .
.

练习册系列答案
相关题目
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了![]() 两种上网学习的月收费方式.
两种上网学习的月收费方式.
收费方式 | 月使用费/元 | 包时上网时间/ | 超时费/(元/ |
| 12 | 40 | 0.5 |
|
|
| 0.6 |
设每月上网学习时间为![]() 小时,方案
小时,方案![]() 的收费金额分别为
的收费金额分别为![]() ,
,![]() .
.
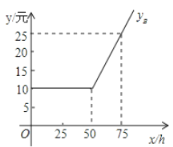
(1)如图是![]() 与
与![]() 之间的函数关系图象,请根据图象填空:
之间的函数关系图象,请根据图象填空:![]() = ;
= ;![]() =
=
(2)求出![]() 与
与![]() (
(![]() )之间的函数关系式.
)之间的函数关系式.
(3)如果每月上网时间为60小时,选择哪种方式网上学习合算,为什么?