题目内容
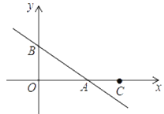
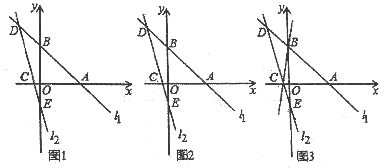
【题目】如图 1，在平面直角坐标系中，直线l1:yx5与x轴，y轴分别交于A.B两点.直线l2:y4xb与l1交于点 D(－3，8)且与x轴，y轴分别交于C、E.
(1)求出点A坐标，直线l2的解析式；
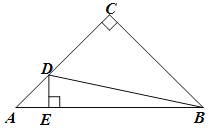
(2)如图2，点P为线段AD上一点(不含端点)，连接CP，一动点Q从C出发，沿线段CP 以每秒1个单位的速度运动到点P，再沿着线段PD以每秒
个单位的速度运动到点D停止，求点Q在整个运动过程中所用最少时间与点P的坐标；
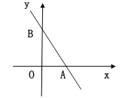
(3)如图3，平面直角坐标系中有一点G(m，2)，使得SCEGSCEB，求点G的坐标.
【答案】（1）A（5，0），y4x-4；
（2）8秒， P（-1,6）；
（3）
.
【解析】
（1）根据l1解析式，y=0即可求出点A坐标，将D点代入l2解析式并解方程，即可求出l2解析式
（2）根据OA=OB可知
ABO和DPQ都为等腰直角三角形，根据路程和速度，可得点Q在整个运动过程中所用的时间为
，当C,P,Q三点共线时，t有最小值，根据矩形的判定和性质可以求出P和Q的坐标以及最小时间.
（3）用面积法
，用含m的表达式求出
，根据SCEGSCEB可以求出G点坐标.
（1）直线l1:yx5，令y=0，则x=5，
故A（5，0）.
将点D(－3，8)代入l2:y4xb，
解得b=-4，
则直线l2的解析式为y4x-4.
∴点A坐标为A（5，0），直线l2的解析式为y4x-4.
（2）如图所示，过P点做y轴平行线PQ，做D点做x轴平行线DQ，PQ与DQ相交于点Q，可知DPQ为等腰直角三角形，
.
依题意有
当C,P,Q三点共线时，t有最小值，此时
故点Q在整个运功过程中所用的最少时间是8秒，此时点P的坐标为（-1,6）.
（3）如图过G做x轴平行线，交直线CD于点H，过C点做CJ⊥HG．
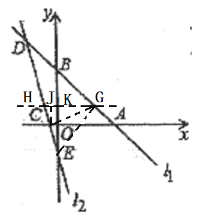
根据l2的解析式，可得点H（
），E（0，－4），C（-1，0）
根据l1的解析式，可得点A（5，0），B（0,5）
则GH=
又SCEGSCEB
所以
,解得
故
