��Ŀ����
����Ŀ����һ��ֱ����������A��B��C����������ij��Ѳ����A��������ֱ�����پ�B ��ʻ��C����ִ�к�Ѳ�������մﵽC������ú�Ѳ����ʻx��h������B�۵ľ���Ϊy��km����y��x�ĺ�����ϵ��ͼ��ʾ��
��1����գ�A��C���ۿڼ�ľ���Ϊ km��![]() ��
��
��2����y��x�ĺ�����ϵʽ���������ͼ�е�P����������ʾ��ʵ�����壻
��3����B����һ����Ϸ����źŵ��źŷ���̨��������źŸ��ǰ뾶Ϊ15km����ú�Ѳ���ܽ��ܵ����źŵ�ʱ���ж��
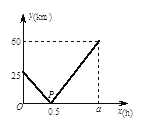
���𰸡���1��85��1.7h��(2) ��0��![]() ��0.5ʱ��y��x�ĺ�����ϵʽΪ��y=-50x+25����0.5��
��0.5ʱ��y��x�ĺ�����ϵʽΪ��y=-50x+25����0.5��![]() ��1.7ʱ��y��x�ĺ�����ϵʽΪ��y=50x��25��(3)�ú�Ѳ���ܽ��ܵ����źŵ�ʱ�� 0.6��h��
��1.7ʱ��y��x�ĺ�����ϵʽΪ��y=50x��25��(3)�ú�Ѳ���ܽ��ܵ����źŵ�ʱ�� 0.6��h��
�����������⣨1����A��B��B��C��ľ�����Ӽ��ɵõ�A��C�����ۿڼ�ľ��룬�������Ѳ�����ٶȣ�Ȼ�����ʱ��=·�����ٶȣ����㼴�����aֵ��
��2����0��x��0.5��0.5��x��1.7���Σ����ô���ϵ������һ�κ�������ʽ��⼴�ɣ�
��3�����ݺ�������ʽ�������Ϊ15kmʱ��ʱ�䣬Ȼ��������ɵý⣮
����������⣺��1����ͼ��֪��A��B�ۿڼ�ľ���Ϊ25��B��C�ۿڼ�ľ���Ϊ60�����ԣ�A��C�ۿڼ�ľ���Ϊ��25+60=85km����Ѳ�����ٶ�Ϊ��25��0.5=50km/h����a=85��50=1.7h��
�ʴ�Ϊ��85��1.7h��
��2����0��x��0.5ʱ����y��x�ĺ�����ϵʽΪ��y=kx+b��������ͼ���㣨0��25������0.5��0������![]() ����ã�
����ã� ![]() �����ԣ�y=��50x+25��
�����ԣ�y=��50x+25��
��0.5��x��1.7ʱ����y��x�ĺ�����ϵʽΪ��y=mx+n��������ͼ���㣨0.5��0������1.7��60������![]() ����ã�
����ã� ![]() �����ԣ�y=50x��25��
�����ԣ�y=50x��25��
��3������50x+25=15�����x=0.2����50x��25=15�����x=0.8��
���ԣ��ú�Ѳ���ܽ��ܵ����źŵ�ʱ��Ϊ��0.6h��

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�