题目内容
【题目】如图,四边形ABCD是平行四边形,E、F是对角线AC上的两点,∠1=∠2.

(1)求证:AE=CF;
(2)求证:四边形EBFD是平行四边形.
【答案】(1)证明见解析;(2)证明见解析.
【解析】(1)通过证明△ADE≌△CBF,由全等三角的对应边相等证得AE=CF。
(2)根据平行四边形的判定定理:对边平行且相等的四边形是平行四边形证得结论。
证明:(1)如图:∵四边形ABCD是平行四边形,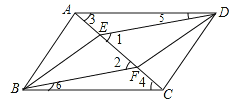
∴AD=BC,AD∥BC,∠3=∠4。
∵∠1=∠3+∠5,∠2=∠4+∠6,
∴∠1=∠2。
∴∠5=∠6。
∵在△ADE与△CBF中,∠3=∠4,AD=BC,∠5=∠6,
∴△ADE≌△CBF(ASA)。
∴AE=CF。
(2)∵∠1=∠2,∴DE∥BF。
又∵由(1)知△ADE≌△CBF,
∴DE=BF。
∴四边形EBFD是平行四边形.
“点睛”本题考查了平行四边形的判定和性质,全等三角形的判定和性质,灵活运用平行四边形的判定定理是解题关键.

练习册系列答案
相关题目