题目内容
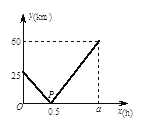
【题目】当前,交通拥堵是城市管理的一大难题.我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用,但为了保证安全,高架桥上最高限速 80 千米/小时.在一般条件下,高架桥上的车流 速度 v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数,当桥上的车流密度达到 180 辆/千 米时,造成堵塞,此时车流速度为 0;当 0≤x≤20 时,桥上畅通无阻,车流速度都为 80 千米/小时, 研究表明:当 20≤x≤180 时,车流速度 v 是车流密度 x 的一次函数.
(1)当 0≤x≤20 和 20≤x≤180 时,分别写出函数 v 关于 x 的函数关系式;
(2)当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)w=x·v可以达到最大,并求出最大值;
(3)某天早高峰(7:30—9:30)经交警部门控制管理,桥上的车流速度始终保持 40 千米/小时,问这天 早高峰期间高架桥分流了多少辆车?
【答案】(1)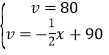 ;(2)当车流密度为90时,车流量最大,最大值为4050辆/小时;(3)这天早高峰期间高架桥分流了8000辆车.
;(2)当车流密度为90时,车流量最大,最大值为4050辆/小时;(3)这天早高峰期间高架桥分流了8000辆车.
【解析】分析:(1)利用速度与车流密度的一次函数关系,代入两组数值(20,80)和(120,0),得到一次函数的参数,根据范围写出分段函数的解析式;
(2)利用车辆数的关系式w=xv,得到其函数关系为二次函数,然后根据二次函数的最值求解即可;
(3)把v=40代入速度与车流密度函数关系,得到车流密度,然后代入求出车流量即可.
详解:(1)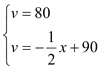
(2)当0≤x≤20时,w=80x
∵k=80﹥0,∴w随x的增大而增大,
∴当x=20时,w最大值=80×20=1600
当20≤x≤180时,![]()
∴当x=90时,w最大值=4050
综合上述两种情况,当x=90时,w最大值=4050
答:当车流密度为90时,车流量最大,最大值为4050辆/小时.
(3)当v=40时,得:![]() ,解得 x=100
,解得 x=100
∴w=100×40=4000 分流了4000×2=8000(辆)
答:这天早高峰期间高架桥分流了8000辆车.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】某校召开运动会,七(1)班学生到超市分两次(第二次少于第一次)购买某种饮料90瓶,共用去205元,已知该种饮料价格如下:
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求:两次分别购买这种饮料多少瓶?
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
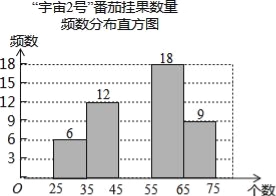
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?