题目内容
【题目】如图AB为⊙O的直径,CD是弦,且AB⊥CD于点E.连结AC、OC、BC.
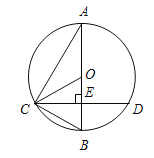
(1)求证:∠ACO=∠BCD;
(2)若EB=2cm,CD=8m,求⊙O的直径.
【答案】(1)详见解析;(2)10
【解析】
(1)根据垂径定理得出弧BC=弧BD,根据圆周角定理得出∠BCD=∠CAB,根据等腰三角形的性质得出∠CAB=∠ACO,即可得出答案;
(2)根据垂径定理求出CE,根据勾股定理求出BC,证△BCE和△BCA相似得出比例式,代入即可求出答案.
(1)证明:∵AB⊥CD,AB过O,
∴弧BC=弧BD,
∴∠BCD=∠CAB,
∵OA=OC,
∴∠CAB=∠ACO,
∴∠ACO=∠BCD;
(2)解:∵AB⊥CD,AB过O,CD=8m,
∴CE=DE=4m,
在Rt△CEB中,由勾股定理得:BC=![]() (m),
(m),
∵AB为直径,AB⊥CD,
∴∠BCA=∠CEB=90°,
∵∠B=∠B,
∴△BEC∽△BCA,
∴![]() ,
,
∴BA=![]() =10(m),
=10(m),
即⊙O的直径是10m.

【题目】垫球是排球队常规训练的重要项目之一,也是我市初中体育学业水平考试的一个选考项目.下列图表中的数据是从九年级一班、二班各随机抽取五名学生垫球测试成绩:
测试学生序号 | ① | ② | ③ | ④ | ⑤ |
一班 | 7 | 8 | 6 | 7 | 7 |
二班 | 4 | 8 | 7 | 10 | 6 |
解答下列问题:
(1)一班五名学生的测试成绩的众数是 ,二班五名学生的测试成绩的中位数是 .
(2)请你在图中补全二班五名学生的垫球测试成绩的折线统计图.从题中的信息,估计 班的垫球成绩要稳定.
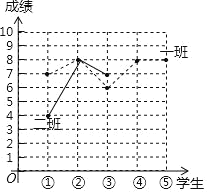
(3)把前三次对应序号下一班学生的垫球测试成绩减去二班学生垫球测试成绩,分别可得到数字3、0、﹣1,从这三个数中任意选取两个数组成有序数对(x,y),请用列表法或画树状图法列出可能出现的结果,并计算点(x,y)落在二次函数y=x2﹣1的图象上的概率.