Question

【题目】如图，已知正方形的边长为，是边上一点，，将，分别沿折痕，向内折叠，点，在点处重合，过点作，交的延长线于.则下列结论正确的有（ ）

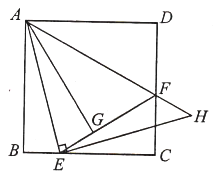
①；②为等腰直角三角形；③点是的中点；④.

A.个B.个C.个D.个

Answer 1

【答案】C

【解析】

由折叠性质易得，∠EAF=45°，结合，可判断②，设DF=x，利用折叠性质可得GF=x，在Rt△ECF中，利用勾股定理建立方程可求出x=，然后可判断③正确，由边长比例关系，可判断①，在等腰直角△AEH中，计算出AH，减去AF即可得FH，从而判断④.

由折叠的性质可得，

∠BAE=∠EAG，∠GAF=∠FAD，

∵∠BAD=90°，

∴∠BAE+∠EAG+∠GAF+∠FAD=90°，

∴2（∠EAG+∠GAF）=90°，

即∠EAF=45°，

又∵EH⊥AE，

∴∠AEH=90°，

∴△AEH为等腰直角三角形，故②正确；

设DF=x，由折叠的性质可得GF=x，EG=BE=1，

∴EF=GF+EG=x+1

∵正方形的边长为

∴CF=3-x,EC=3-1=2,

在Rt△ECF中，由勾股定理得，

解得：

∴，故③正确；

在△ADF和△ECF中，

AD=3，DF=，EC=2，CF=，∠ADF=∠ECF=90°，

∵，，

∴△ADF和△ECF不相似，故①错误；

在Rt△ABE中，

在等腰Rt△AEH中，，

在Rt△ADF中，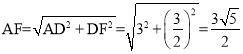

∴，故④正确，

综上所述，②③④正确，故选C.