题目内容
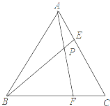
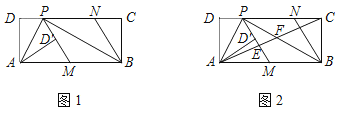
【题目】如图1,在矩形ABCD中,P为CD边上一点(DP<CP),∠APB=90°.将△ADP沿AP翻折得到△AD′P,PD′的延长线交边AB于点M,过点B作BN∥MP交DC于点N.
(1)求证:AD2=DPPC;
(2)请判断四边形PMBN的形状,并说明理由;
(3)如图2,连接AC分别交PM、PB于点E、F.若AD=3DP,探究EF与AE之间的的数量关系.
【答案】(1)见解析;(2)四边形PMBN是菱形;理由见解析;(3)![]() .
.
【解析】
(1)过点P作PG⊥AB于点G,易知四边形DPGA,四边形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易证△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
(2)DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB∠PAM=∠APB∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
(3)由于AD=3DP,可设设DP=1,则AD=3,由(1)可知:AG=DP=1,PG=AD=3,从而求出BG=PC=9,AB=AG+BG=10,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得![]() =
=![]() ,
,![]() =
=![]() ,从而可求出EF=AF﹣AE=
,从而可求出EF=AF﹣AE=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,从而可得
AC,从而可得![]() =
= =
=![]() .
.
(1)证明:过点P作PG⊥AB于点G,如图1所示:

则四边形DPGA和四边形PCBG是矩形,
∴AD=PG,DP=AG,BG=PC,
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() =
=![]() ,
,
∴PG2=AGBG,
即AD2=DPPC;
(2)解:四边形PMBN是菱形;理由如下:
∵四边形ABCD是矩形,
∴AB∥CD,
∵BM∥PN,BN∥MP,
∴四边形PMBN是平行四边形,
∵DP∥AB,
∴∠DPA=∠PAM,
由题意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB﹣∠PAM=∠APB﹣∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
∴四边形PMBN是菱形;
(3)解:∵AD=3DP,
∴设DP=1,则AD=3,
由(1)可知:AG=DP=1,PG=AD=3,
∵PG2=AGBG,
∴32=1BG,
∴BG=PC=9,
AB=AG+BG=10,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∵PM=MB,
∴∠MPB=∠MBP,
∵∠APB=90°,
∴∠MPB+∠APM=∠MBP+∠MAP=90°,
∴∠APM=∠MAP,
∴PM=MA=MB,
∴AM=![]() AB=5,
AB=5,
∵AB∥CD,
∴△PCE∽△MAE,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴EF=AF﹣AE=![]() AC﹣
AC﹣![]() AC=
AC=![]() AC,
AC,
∴![]() =
= =
=

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案