题目内容
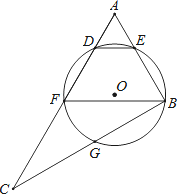
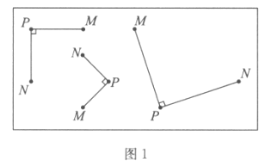
【题目】如图1中的三种情况所示,对于平面内的点M,点N,点P,如果将线段PM绕点P顺时针旋转90°能得到线段PN,就称点N是点M关于点P的“正矩点”.
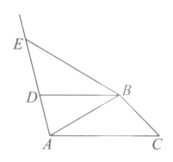
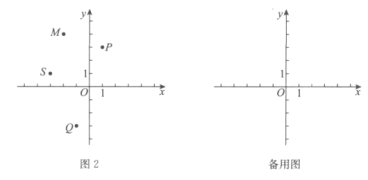
(1)在如图2所示的平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() .
.
①在点P,点Q中,___________是点S关于原点O的“正矩点”;
②在S,P,Q,M这四点中选择合适的三点,使得这三点满足:
点_________是点___________关于点___________的“正矩点”,写出一种情况即可;
(2)在平面直角坐标系![]() 中,直线
中,直线![]() 与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为
与x轴交于点A,与y轴交于点B,点A关于点B的“正矩点”记为点C,坐标为![]() .
.
①当点A在x轴的正半轴上且OA小于3时,求点C的横坐标![]() 的值;
的值;
②若点C的纵坐标![]() 满足
满足![]() ,直接写出相应的k的取值范围.
,直接写出相应的k的取值范围.
【答案】(1)①点P;②见解析;(2)①点C的横坐标![]() 的值为-3;②
的值为-3;②![]()
【解析】
(1)①在点P,点Q中,点OS绕点O顺时针旋转90°能得到线段OP,故S关于点O的“正矩点”为点P;
②利用新定义得点S是点P关于点M的“正矩点”(答案不唯一);
(2)①利用新定义结合题意画出符合题意的图形,利用新定义的性质证明△BCF≌△AOB,则FC=OB求得点C的横坐标;
②用含k的代数式表示点C纵坐标,代入不等式求解即可.
解:(1)①在点P,点Q中,点OS绕点O顺时针旋转90°能得到线段OP,故S关于点O的“正矩点”为点P,
故答案为点P;
②因为MP绕M点顺时针旋转![]() 得MS,所以点S是点P关于点M的“正矩点”,同理还可以得点Q是点P关于点S的“正矩点”.(任写一种情况就可以)
得MS,所以点S是点P关于点M的“正矩点”,同理还可以得点Q是点P关于点S的“正矩点”.(任写一种情况就可以)
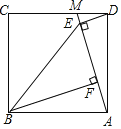
(2)①符合题意的图形如图1所示,作CE⊥x轴于点E,CF⊥y轴于点F,可得
∠BFC=∠AOB=90°.
∵直线![]() 与x轴交于点A,与y轴交于点B,
与x轴交于点A,与y轴交于点B,
∴点B的坐标为![]() 在x轴的正半轴上,
在x轴的正半轴上,
∵点A关于点B的“正矩点”为点![]() ,
,
∴∠ABC=90°,BC=BA,
∴∠1+∠2=90°,
∵∠AOB=90°,
∴∠2+∠3=90°,
∴∠1=∠3.
∴△BFC≌△AOB,
∴![]() ,
,
可得OE=3.
∵点A在x轴的正半轴上且![]() ,
,
![]() ,
,
∴点C的横坐标![]() 的值为-3.
的值为-3.
②因为△BFC≌△AOB,![]() ,A在
,A在![]() 轴正半轴上,
轴正半轴上,
所以BF=OA,所以OF=OB-OF=![]()
点![]() ,如图2, -1<
,如图2, -1<![]() ≤2,
≤2,
即:-1<![]() ≤2,
≤2,
则![]() .
.