题目内容
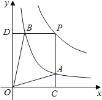
【题目】如图,在△ABC中,∠BAC=30°,∠ACB=45°,BD∥AC,BD=AB,且C,D两点位于AB所在直线两侧,射线AD上的点E满足∠ABE=60°.
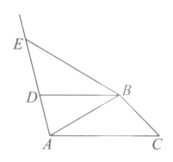
(1)∠AEB=___________°;
(2)图中与AC相等的线段是_____________,证明此结论只需证明△________≌△_______.
【答案】45 BE ABC BDE
【解析】
(1)由平行线和等腰三角形的性质得出∠BDA=∠BAD=75°,求出∠DBE=∠ABE-∠ABD=30°,由三角形的外角性质即可得出答案; (2)证出△ABC≌△BDE(AAS),得出AC=BE;即可得出答案.
解:(1)∵BD∥AC,
∴∠ABD=∠BAC=30°, ∵BD=AB,
∴∠BDA=∠BAD=![]() (180°-30°)=75°,
(180°-30°)=75°,
∵∠ABE=60°, ∴∠DBE=∠ABE-∠ABD=30°,
∴∠AEB=∠ADB-∠DBE=75°-30°=45°;
故答案为:45°;
(2)在△ABC和△BDE中,

∴△ABC≌△BDE(AAS),
∴AC=BE;
故答案为:BE,ABC,BDE.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目