题目内容
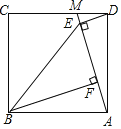
【题目】如图,点M是正方形ABCD边CD上一点,连接AM,作DE⊥AM于点E,BF⊥AM于点F,连接BE.
(1)求证:AE=BF;
(2)已知AF=2,四边形ABED的面积为24,求EF:BF的值.
【答案】(1)见解析;(2)![]()
【解析】
(1)根据正方形的性质得到BA=AD,∠BAD=90°,再根据DE⊥AM于点E,BF⊥AM于点F,等量代换得到∠ABF=∠DAE,即可证明△ABF≌△DAE(AAS),利用全等三角形的性质即可得到AE=BF;
(2)设AE=x,则BF=x,DE=AF=2,根据四边形ABED的面积为24,列出方程即可解答.
(1)证明:∵四边形ABCD为正方形,
∴BA=AD,∠BAD=90°,
∵DE⊥AM于点E,BF⊥AM于点F,
∴∠AFB=90°,∠DEA=90°,
∵∠ABF+∠BAF=90°,∠EAD+∠BAF=90°,
∴∠ABF=∠DAE,
在△ABF和△DAE中
∠BFA=∠DEA,∠ABF=∠EAD,AB=DA,
∴△ABF≌△DAE(AAS),
∴BF=AE;
(2)设AE=x,则BF=x,DE=AF=2,
∵四边形ABED的面积为24,
∴S四边形ABED=S△ABE+S△ADE,
即![]() xx+
xx+![]() x2=24,
x2=24,
解得x1=6,x2=8(舍去),
∴EF=x2=4,BF=6
∴![]()

【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.