题目内容
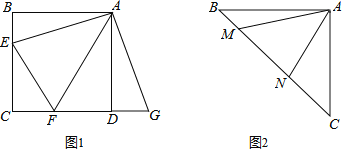
【题目】如图,在Rt△ABC中,∠ABC=90°,点F为AC中点,⊙O经过点B,F,且与AC交于点D,与AB交于点E,与BC交于点G,连结BF,DE,弧EFG的长度为(1+![]() )π.
)π.
(1)求⊙O的半径;
(2)若DE∥BF,且AE=a,DF=2+![]() ﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
﹣a,请判断圆心O和直线BF的位置关系,并说明理由.
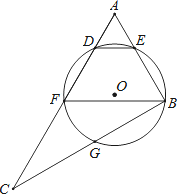
【答案】(1)r=1+![]() ;(2)圆心O在直线BF上.理由见解析.
;(2)圆心O在直线BF上.理由见解析.
【解析】
(1)设⊙O的半径为r,再根据弧长公式即可得出结论;
(2)先根据DE∥BF得出∠ADE=∠AFB,再根据圆内接四边形的性质得出∠AFB+∠DEB=180°,进而得出AF的长.在Rt△ABC中,根据直角三角形的性质求出BF的长,再由B、F都在⊙O上即可得出结论.
(1)设⊙O的半径为r,
∵∠ABC=90°
∴弧EFG所对的圆心角的度数为180°,
∴![]() =(1+
=(1+![]() )π,即r=1+
)π,即r=1+![]() ;
;
(2)答:圆心O在直线BF上.
理由如下:
∵DE∥BF,
∴∠ADE=∠AFB.
∵四边形DEBF是⊙O的内接四边形,
∴∠AFB+∠DEB=180°.
∵∠AED+∠DEB=180°,
∴∠AFB=∠AED,
∴∠ADE=∠AED,
∴AD=AE=a.
∵DF=2+![]() ﹣a,
﹣a,
∴AF=AD+DF=2+![]() .
.
在Rt△ABC中,∠ABC=90°且F为AC中点,
∴BF=AF=2+![]() .
.
∵r=1+![]() ,
,
∴BF=2r.
∵B、F都在⊙O上,
∴BF为⊙O直径,
∴点O在直线BF上.

 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案【题目】王老师将![]() 个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
个黑球和若干个白球放入一个不透明的口袋并搅匀,让若干学生进行摸球实验,每次摸出一个球(有放回),下表是活动进行中的一组统计数据.
摸球的次数 |
|
|
|
|
|
|
摸到黑球的次数 |
|
|
|
|
|
|
摸到黑球的频率 |
|
|
|
|
|
![]() 补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
补全上表中的有关数据,根据上表数据估计从袋中摸出一个球是黑球的概率是________(精确到0.01);
![]() 估算袋中白球的个数;
估算袋中白球的个数;
![]() 在
在![]() 的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
的条件下,若小强同学有放回地连续两次摸球,用画树状图或列表的方法计算他两次都摸出白球的概率.
【题目】[问题情境]
已知矩形的面积为一定值1,当该矩形的一组邻边分别为多少时,它的周长最小?最小值是多少?
[数学模型]
设该矩形的一边长为x,周长为L,则L与x的函数表达式为 .
[探索研究]
小彬借鉴以前研究函数的经验,先探索函数![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数![]() 的自变量x的取值范围是 ,
的自变量x的取值范围是 ,
如表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①直接写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y的最小值为 .
[解决问题]
(2)直接写出“问题情境”中问题的结论.