题目内容
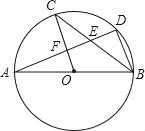
【题目】如图，矩形
的对角线相交于点
，
，
.
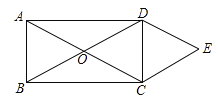
（1）求证：四边形
是菱形；
（2）若
，
，求矩形的面积.
【答案】（1）见解析；（2）
【解析】
（1）首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形，再根据矩形的性质可得OC=OD，即可利用一组邻边相等的平行四边形是菱形判定出结论；
（2）由菱形的性质可得OC=OD=DE=2，∠E=∠DOC=60°，可得BD=4，△OCD是等边三角形，可得CD=2，由勾股定理可求BC的长，即可求矩形ABCD的面积．
（1）∵
，
,
∴四边形
是平行四边形,
∵四边形
是矩形,
∴
，
，
,
∴
,
∴平行四边形是菱形;
（2）∵四边形是菱形,
∴
，
，
∴
,
∵
，（已证）,
∴
是等边三角形,
∴
,
∵矩形中，
,
∴
,
∴矩形的面积：
.
练习册系列答案
相关题目
【题目】某公司为一种新型电子产品在该城市的特约经销商，已知每件产品的进价为40元，该公司每年销售这种产品的其他开支（不含进货价）总计100万元，在销售过程中得知，年销售量y（万件）与销售单价x（元）之间存在如表所示的函数关系，并且发现y是x的一次函数．
销售单价x（元） | 50 | 60 | 70 | 80 |
销售数量y（万件） | 5.5 | 5 | 4.5 | 4 |
（1）求y与x的函数关系式；
（2）问：当销售单价x为何值时，该公司年利润最大？并求出这个最大值；
【备注：年利润=年销售额﹣总进货价﹣其他开支】
（3）若公司希望年利润不低于60万元，请你帮助该公司确定销售单价的范围．
