题目内容
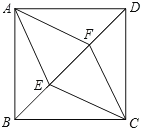
【题目】如图,正方形ABCD的边长为2![]() ,点E、F在BD上,且DF=BE=1,四边形AECF的面积为______.
,点E、F在BD上,且DF=BE=1,四边形AECF的面积为______.
【答案】4.
【解析】
连结AC,交BD于点O,依据正方形的性质可得到AC⊥EF,然后再证明OE=OF,从而可得到四边形AFCE为平行四边形,于是可证明它是一个菱形;先求得BF的长,然后可得到OF的长,进而可得到EF的长,依据依据菱形的面积等于两对角线乘积的一半求解即可.
解:连结AC,交BD于点O.
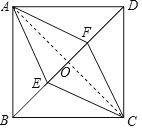
∵四边形ABCD是正方形,
∴OA=OC,OB=OD.
又∵BE=DF,
∴BE﹣BO=DF﹣DO即OE=OF,
∴四边形AFCE是平行四边形.
又∵AC⊥EF,
∴四边形AFCE是菱形.
∵AB=AD=2![]() ,
,
∴由勾股定理可知AC=BD=4.
∵DF=BE=1,
∴EF=2,
∴菱形的面积=![]() EFAC=
EFAC=![]() ×2×4=4.
×2×4=4.
故答案为:4.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目