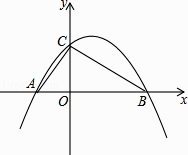
题目内容
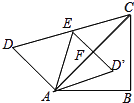
【题目】如图,将一副直角三角板拼在一起得四边形ABCD,∠ACB=45°,∠ACD=30°,点E为CD边上的中点,连接AE,将△ADE沿AE所在直线翻折得到△AD′E,D′E交AC于F点,若AB= 6![]() cm,点D′到BC的距离是( )
cm,点D′到BC的距离是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
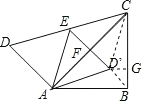
【解析】连接CD′,BD′,过点D′作D′G⊥BC于点G,进而得出△ABD′≌△CBD′,于是得到∠D′BG=45°,D′G=GB,进而利用勾股定理求出点D′到BC边的距离.
连接CD′,BD′,过点D′作D′G⊥BC于点G,
∵AC垂直平分线ED′,
∴AE=AD′,CE=CD′,
∵AE=EC,∴AD′=CD′=4![]() ,
,
在△ABD′和△CBD′中,
AB=BCBD′=BD′AD′=CD′,
∴△ABD′≌△CBD′(SSS),
∴∠D′BG=45°,
∴D′G=GB,
设D′G长为xcm,则CG长为(6![]() x)cm,
x)cm,
在Rt△GD′C中
x2+(6![]() x)2=(4
x)2=(4![]() )2,
)2,
解得:x1=3![]() 6,x2=3
6,x2=3![]() +6(舍去),
+6(舍去),
∴点D′到BC边的距离为(3![]() 6)cm.
6)cm.
故选:C.

 阅读快车系列答案
阅读快车系列答案【题目】甲、乙两校的学生人数基本相同,为了解这两所学校学生的数学学业水平,在同一次测试中,从两校各随机抽取了30名学生的测试成绩进行调查分析,其中甲校已经绘制好了条形统计图,乙校只完成了一部分.
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
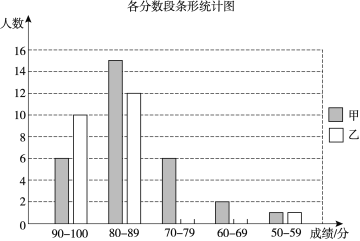
(1)请根据乙校的数据补全条形统计图;
(2)两组样本数据的平均数、中位数、众数如下表所示,请补全表格;
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
(3)两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些,
请为他们各写出一条可以使用的理由;
甲校: .乙校: .
(4)综合来看,可以推断出 校学生的数学学业水平更好一些,理由为 .
【题目】阅读理解:德国著名数学家高斯被认为是历史上最重要的数学家之一,并有"数学王子"的美誉.高斯从小就善于观察和思考.在他读小学时候就能在课堂上快速的计算出![]() ,今天我们可以将高斯的做法归纳如下:
,今天我们可以将高斯的做法归纳如下:
令![]() ①
①
![]() ②
②
(右边相加100+1=2+99=3+98=…..=100+1共100组)
①+②:有2S=101x100 解得:![]()
(1)请参照以上做法,回答,3+5+7+9+…..+97= ;
请尝试解决下列问题:
如下图,有一个形如六边形的点阵,它的中心是一个点,算第一层,第二层每边有两个点,第三层每边有三个点,依此类推.

(2)填写下表:
层数 | 1 | 2 | 3 | 4 |
该层对应的点数 | 1 | 6 | 12 | 18 |
所有层的总点数的和 | 1 | 7 | 19 |
①写出第n层所对应的点数;(n≥2)
②如果某一层共96个点,求它是第几层;
③写出n层的六边形点阵的总点数.
【题目】已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.

(1)求∠MON的大小.
(2)当锐角∠AOC的大小发生改变时,∠MON的大小是否发生改变?为什么?
【题目】随着我市社会经济的发展和交通状况的改善,我市的旅游业得到了高速发展![]() 某旅游公司对我市一企业个人旅游年消费情况进行问卷调查
某旅游公司对我市一企业个人旅游年消费情况进行问卷调查![]() 随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
随机抽取部分员工,记录每个人年消费金额,并将调查数据适当整理,绘制成如下两幅尚不完整的表和图:
组别 | 个人年消费金额 | 频数 | 频率 |
A |
| 18 |
|
B |
| a | b |
C |
|
|
|
D |
| 24 |
|
E |
| 12 |
|
合计 | c |
| |

根据以上信息解答下列问题:
![]() ________;
________; ![]() ________;
________; ![]() ________;
________;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.
若这个企业有3000名员工,请你估计个人旅游年消费金额在6000元以上的人数.