题目内容
【题目】如图,在△ABC中,∠ACB=90°,AC=8,BC=6,分别以AB、BC、CA为一边向形外作正方形,连接EF、GM、ND, 设△AEF,△CGM,△BND的面积分别为![]() ,
,![]() ,
,![]() ,则
,则![]() =___.
=___.

【答案】72
【解析】
作ER⊥FA交FA的延长线于R,作DH⊥NB交NB的延长线于H,作NT⊥DB交DB的延长线于T,,分别表示出三角形的面积,然后进行计算即可.
解:作ER⊥FA交FA的延长线于R,作DH⊥NB交NB的延长线于H,作NT⊥DB交DB的延长线于T,
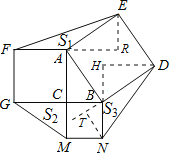
∵分别以△ABC的边AB、BC、CA为一边向△ABC外作正方形ABDE、正方形BCMN、正方形CAFG,
∵AE=AB,∠ARE=∠ACB,∠EAR=∠CAB,
∴△AER≌△ABC,
∴ER=BC=6,FA=AC=8,
∴S1=![]() ER·AF=
ER·AF=![]() ,S2=
,S2=![]() CG·CM=
CG·CM=![]() ,
,
同理可得HD=AR=AC,
∴S1=S2=S3=24.
所以![]()
故答案为:72.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
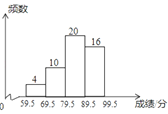
【题目】某中学开展“数学史”知识竞赛活动,八年级(1)、(2)班根据初赛成绩,各选出5名选手参加复赛,两个班各选出的5名选手的复赛成绩(满分为100分)如图所示:
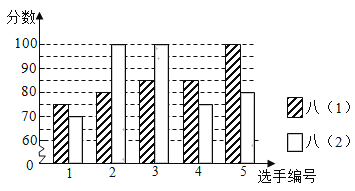
(1)根据图示填写下表a、b、c的值:
统计量 班别 | 平均数(分) | 中位数(分) | 众数(分) |
八年(1)班 | a | 85 | c |
八年(2)班 | 85 | b | 100 |
(2)结合两班复赛成绩的平均数和中位数,分析哪个班的选于复赛成绩较好;
(3)通过计算八年(1)班5名选手的复赛成绩的方差S八(1)2=70,请你计算八年(2)班5名选手复赛成绩的方差并判断哪个班的选手复赛成绩较为均衡.