��Ŀ����
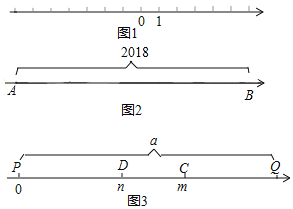
����Ŀ����ͼ��ʾ���������ϵ�A��B��C��ʾ�����ֱ�Ϊ��2��1��6����A���B֮��ľ����ʾΪAB����B���C֮��ľ����ʾΪBC����A���C֮��ľ����ʾΪAC��

��1����AB=�� ��BC=�� ��AC=�� ��
��2����A��B��C��ʼ���������˶�������A��ÿ��1����λ���ȵ��ٶ������˶���ͬʱ����B�͵�C�ֱ���ÿ��2����λ���Ⱥ�5����λ���ȵ��ٶ������˶������ʣ�BC��AB��ֵ�Ƿ������˶�ʱ��t�ı仯���ı䣿���仯����˵�����ɣ������䣬������ֵ��
��3���ɵڣ�1��С����Է��֣�AB+BC=AC������C��ÿ��3����λ���ȵ��ٶ������˶���ͬʱ����A�͵�B�ֱ���ÿ��1����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ������˶������ʣ������˶�ʱ��t�ı仯��AB��BC��AC֮���Ƿ���������ڣ�1����������ϵ����˵�����ɣ�
���𰸡���1��3,5,8����2��![]() ��ֵ��������ʱ��t�ı仯���ı䣻��3���������.
��ֵ��������ʱ��t�ı仯���ı䣻��3���������.
��������
��1�����ݵ�A��B��C�������ϵ�λ�ã�д��AB��BC��AC�ij��ȣ�
��2�����BC��AB��ֵ��Ȼ�����BC-AB��ֵ���жϼ��ɣ�
��3���ֱ��ʾ��AB��BC��AC�ij��ȣ�Ȼ���������۵ó�֮��Ĺ�ϵ��
(1)��ͼ�ɵ�,![]() ,
,![]()
![]()
�ʴ�Ϊ:3,5,8;
(2)![]() ,
,
��![]() ��ֵ��������ʱ��t�ı仯���ı�;
��ֵ��������ʱ��t�ı仯���ı�;
(3)�������,![]() ,
,
![]() ʱ)��
ʱ)��![]() ��,
��,
![]() ʱ)��
ʱ)��![]() ��,
��,
��![]() ʱ,
ʱ,![]() ,
,
��![]() ʱ,
ʱ,![]() ,
,
��![]() ʱ,
ʱ,![]()

 ������ʱͬ����ϰ��ϵ�д�
������ʱͬ����ϰ��ϵ�д�