题目内容
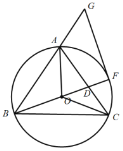
【题目】如图,![]() 是⊙
是⊙![]() 的直径,弦
的直径,弦![]() 于
于![]() ,点
,点![]() 在弧
在弧![]() 上(不含端点
上(不含端点![]() ), 连接
), 连接![]()
![]()
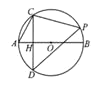
(1)图中有无和![]() 相等的线段,并证明你的结论.
相等的线段,并证明你的结论.
(2)求![]() 的值。
的值。
【答案】(1)图中![]() .理由见解析;(2)
.理由见解析;(2)![]() .
.
【解析】
(1)连接![]() ,根据同弧所对的圆周角相等,可得
,根据同弧所对的圆周角相等,可得![]() ,即得
,即得![]() .根据垂径定理可得
.根据垂径定理可得![]() ,由于
,由于![]() , 即得
, 即得![]() ,从而可得
,从而可得![]() .
.
(2)作直径![]() ,连接
,连接![]() .根据圆周角定理,可得
.根据圆周角定理,可得![]() ,
,![]() ,由
,由![]() , 即得
, 即得 ![]() , 设
, 设![]() .则
.则![]() ,即得
,即得![]() ,利用(1)结论,可得
,利用(1)结论,可得![]() ,由
,由![]() ,继而求出
,继而求出![]() ,利用勾股定理可求出
,利用勾股定理可求出![]() ,由
,由![]() ,即可得出
,即可得出![]() 的值.
的值.
(1)解:图中![]() .理由如下:
.理由如下:
连接![]() ,则
,则![]() .
.
∴![]()
∵![]() 是直径,
是直径,![]() ,
,![]() .
.
∴![]() ,∴
,∴![]()
∴![]()
(2)解:作直径![]() ,连接
,连接![]() .
.
则![]() ,
,![]() .
.
∴![]() ,
, ![]() 设
设![]() .则
.则![]() .
.
∴![]() .
.
由(1),![]() .
.
∴![]() ∴
∴![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
∴![]()
∴![]() .
.
故答案为:(1)图中![]() .理由见解析;(2)
.理由见解析;(2)![]() .
.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目