��Ŀ����
����Ŀ����ȫ��������ѧ�����У�������������ѧ���ijɼ����÷־�Ϊ����������������ֳ����飬���Ƴ����µ�Ƶ�ʷֲ�ֱ��ͼ����ͼ��ʾ������֪ͼ�д����ҵĵ�һ�����������ġ�����С���Ƶ�ʷֱ���0��25��0��15��0��10��0��10���ڶ����Ƶ����40��

��1���ڶ�С���Ƶ����_____������ȫ���Ƶ�ʷֲ�ֱ��ͼ��
��2���������������ѧ��������_________��
��3�������������ѧ���ijɼ�����λ�����ڵ�______���ڣ�������˵�����ɣ�
���𰸡�0.4 100 ��
��������
��1��1��ȥ�������Ƶ�ʼ��ɣ�
��2���ڶ���Ƶ�����Եڶ���Ƶ�ʣ�
��3���ɵ�һ������Ƶ��֮��Ϊ0.25+0.4=0.65��0.5֪ǰ���������֮�ͳ���������������λ���Ķ������ɵã�
�⣺��1���ڶ�С��Ƶ��Ϊ1-��0.25+0.15+0.10+0.10��=0.4��
�ڶ���С���εĸ߶�ӦΪ�������4������ͼ��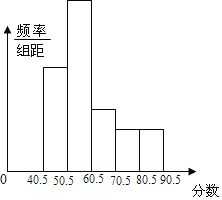
�ʴ�Ϊ��0.4��
��2���������������ѧ��������40��0.4=100�ˣ�
�ʴ�Ϊ��100��
��3���ߵ�һ������Ƶ��֮��Ϊ0.25+0.4=0.65��0.5��
����λ�����ڵڶ�С�飬
�ʴ�Ϊ������

����Ŀ��ij�̳�ͬʱ�����ס���������Ʒ��100��������ۺ��ۼ����±���
��Ʒ���� | �� | �� |
����(Ԫ/��) | 40 | 90 |
�ۼ�(Ԫ/��) | 60 | 120 |
�����м�����Ʒ����x�����̳�������100����Ʒ��������ΪyԪ��
(��)д��y����x�ĺ�����ϵʽ��
(��)���̳��ƻ����Ͷ��8000Ԫ���ڹ�����������Ʒ��
������Ҫ�������ټ�����Ʒ��
������������Щ��Ʒ�����̳��ɻ�õ���������Ƕ���Ԫ��