Question

【题目】如图，正方形的边长为，在正方形外，，过作于，直线，交于点，直线交直线于点，则下列结论正确的是（ ）

①；②；③；

④若，则

A.1个B.2个C.3个D.4个

Answer 1

【答案】C

【解析】

①利用等腰三角形的性质即可证明．②根据DA=DC=DE，利用圆周角定理可知∠AEC=∠ADC=45°，即可解决问题．③如图，作DF⊥DM交PM于F，证明△ADM≌△CDF（SAS）即可解决问题．④解直角三角形求出CE=EF=可得结论．

∵四边形ABCD是正方形，

∴DA=DC,∠ADC=90°，

∵DC=DE，

∴DA=DE，

∴∠DAE=∠DEA，故①正确，

∵DA=DC=DE，

∴∠AEC=∠ADC=45°(圆周角定理)，

∵DM⊥AE，

∴∠EHM=90°，

∴∠DMC=45°，故②正确，

如图，作DF⊥DM交PM于F，

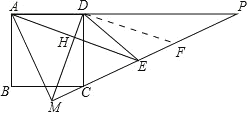
∵∠ADC=∠MDF=90°，

∴∠ADM=∠CDF，

∵∠DMF=45°，

∴∠DMF=∠DFM=45°，

∴DM=DF，∵DA=DC，

∴△ADM≌△CDF(SAS)，

∴AM=CF，

∴AM+CM=CF+CM=MF=DM，

∴=，故③正确，

若MH=2,则易知AH=MH=HE=2,AM=EM=2，

在Rt△ADH中, ，

∴DM=3,AM+CM=3，

∴CM=CE=，

∴S△DCM=S△DCE，故④错误，

故选C.