题目内容
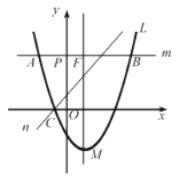
【题目】如图,抛物线y=-![]() x2+bx+c,与
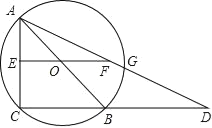
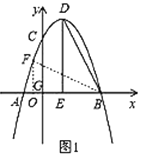
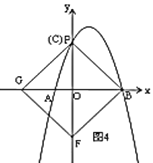
x2+bx+c,与![]() 轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
轴交于点A和点B,与y轴交于点C,点B坐标为(6,0),点C坐标为(0,6),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.
(Ⅰ)求抛物线的解析式及点D的坐标;
(Ⅱ)点![]() 是抛物线上的动点,当
是抛物线上的动点,当![]() 时,求点F坐标;
时,求点F坐标;
(Ⅲ)若点P是x轴上方抛物线上的动点,以PB为边作正方形PBFG,随着点P的运动,正方形的大小、位置也随着改变,当顶点F或G恰好落在y轴上时,请直接写出点P的横坐标.

【答案】(Ⅰ)y=-![]() x2+2x+6;
x2+2x+6;![]() ;(Ⅱ)
;(Ⅱ)![]() 点的坐标为
点的坐标为![]() 或
或![]() ;(Ⅲ)点
;(Ⅲ)点![]() 的横坐标为
的横坐标为![]() 或4或0.
或4或0.
【解析】
(Ⅰ)把B、C坐标代入y=-![]() x2+bx+c,解方程组求出b、c的值即可得抛物线解析式,把解析式变形为顶点式可得D点坐标;(Ⅱ)过F作FG⊥x轴于点G,设F点坐标为
x2+bx+c,解方程组求出b、c的值即可得抛物线解析式,把解析式变形为顶点式可得D点坐标;(Ⅱ)过F作FG⊥x轴于点G,设F点坐标为![]() ,利用△FBG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,即可求得F点的坐标;(Ⅲ)设
,利用△FBG∽△BDE,由相似三角形的性质可得到关于F点坐标的方程,即可求得F点的坐标;(Ⅲ)设![]() ,分G在y轴上、F在y轴上、F在y轴上,P与C重合三种情况讨论,根据正方形的性质得出m的方程,求出m的值即可得P点横坐标.
,分G在y轴上、F在y轴上、F在y轴上,P与C重合三种情况讨论,根据正方形的性质得出m的方程,求出m的值即可得P点横坐标.
(Ⅰ)把点![]() 坐标为(6,0),点
坐标为(6,0),点![]() 坐标为(0,6)代入抛物线y=-
坐标为(0,6)代入抛物线y=-![]() x2+bx+c
x2+bx+c
得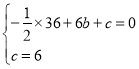 ,解得
,解得![]() .
.
∴![]() ,
,
∴![]() .
.
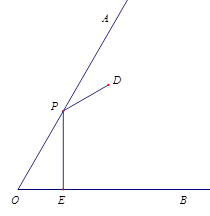
(Ⅱ)如图1,过![]() 作
作![]() 轴于点
轴于点![]() ,
,
设![]() ,则
,则![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴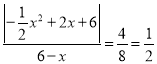 ,
,
当点![]() 在
在![]() 轴上方时,有
轴上方时,有![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
此时![]() 点坐标为
点坐标为![]() .
.
当点![]() 在
在![]() 轴下方时,有
轴下方时,有![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
此时![]() 点坐标为
点坐标为![]() .
.
综上可知![]() 点的坐标为
点的坐标为![]() 或
或![]() .
.
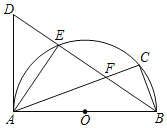
(Ⅲ)设![]() ,有三种情况:
,有三种情况:
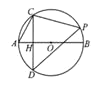
①如图2,当![]() 在
在![]() 轴上时,过P作
轴上时,过P作![]() 轴于
轴于![]() ,作PM⊥x轴于
,作PM⊥x轴于![]() ,
,
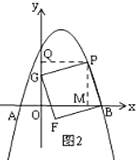
∵四边形![]() 是正方形,
是正方形,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ≌△PMB,
≌△PMB,
∴![]() .
.
即![]() ,解得
,解得![]() ,
,![]() (舍).
(舍).
∴![]() 的横坐标为
的横坐标为![]() .
.
②当![]() 在
在![]() 轴上时,如图3,过
轴上时,如图3,过![]() 作PM⊥x轴于M,
作PM⊥x轴于M,
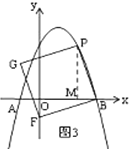
同理得:△PMB≌![]() ,
,
∴OB=PM=6.
即![]() ,解得:
,解得:![]() (舍),
(舍),![]() .
.
∴![]() 的横坐标为4.
的横坐标为4.
③当![]() 在
在![]() 轴上时,如图4,此时
轴上时,如图4,此时![]() 与
与![]() 重合,此时
重合,此时![]() 的横坐标为0.
的横坐标为0.
综上所述,点![]() 的横坐标为
的横坐标为![]() 或4或0.
或4或0.

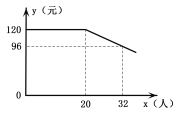
【题目】某商场的运动服装专柜,对![]() 两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
两种品牌的远动服分两次采购试销后,效益可观,计划继续采购进行销售.已知这两种服装过去两次的进货情况如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累计采购款/元 | 10200 | 14400 |
(1)问![]() 两种品牌运动服的进货单价各是多少元?
两种品牌运动服的进货单价各是多少元?
(2)由于![]() 品牌运动服的销量明显好于
品牌运动服的销量明显好于![]() 品牌,商家决定采购
品牌,商家决定采购![]() 品牌的件数比
品牌的件数比![]() 品牌件数的
品牌件数的![]() 倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件
倍多5件,在采购总价不超过21300元的情况下,最多能购进多少件![]() 品牌运动服?
品牌运动服?