题目内容
【题目】如图,在平面直角坐标系中,点![]() 为坐标原点,
为坐标原点,![]() ,点
,点![]() 的坐标分别为
的坐标分别为![]() ,动点
,动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动;动点
个单位的速度运动;动点![]() 从点
从点![]() 沿
沿![]() 以每秒
以每秒![]() 个单位的速度运动.
个单位的速度运动.![]() 同时出发,设运动时间为
同时出发,设运动时间为![]() 秒.
秒.
(1)在![]() 时,
时,![]() 点坐标 ,
点坐标 ,![]() 点坐标 ;
点坐标 ;
(2)当![]() 为何值时,四边形
为何值时,四边形![]() 是矩形?
是矩形?
(3)运动过程中,四边形![]() 能否为菱形?若能,求出
能否为菱形?若能,求出![]() 的值;若不能,说明理由.
的值;若不能,说明理由.
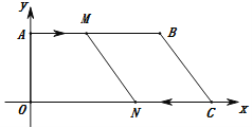
【答案】(1)M(3,8) N(15,0) ;(2)t=7 ;(3)能,t=5 .
【解析】
(1)根据点B、C的坐标求出AB、OA、OC,然后根据路程=速度×时间求出AM、CN,再求出ON,然后写出点M、N的坐标即可;
(2)根据有一个角是直角的平行四边形是矩形,当AM=ON时,四边形OAMN是矩形,然后列出方程求解即可;
(3)先求出四边形MNCB是平行四边形的t值,并求出CN的长度,然后过点B作BC⊥OC于D,得到四边形OABD是矩形,根据矩形的对边相等可得OD=AB,BD=OA,然后求出CD,再利用勾股定理列式求出BC,然后根据邻边相等的平行四边形是菱形进行验证.
解:(1)∵B(15,8),C(21,0),
∴AB=15,OA=8,
OC=21,
当t=3时,AM=1×3=3,
CN=2×3=6,
∴ON=OC-CN=21-6=15,
∴点M(3,8),N(15,0);
故答案为:(3,8);(15,0);
(2)当四边形OAMN是矩形时,AM=ON,
∴t=21-2t,
解得t=7秒,
故t=7秒时,四边形OAMN是矩形;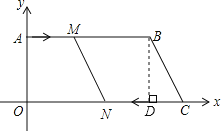
(3)存在t=5秒时,四边形MNCB为菱形.
理由如下:四边形MNCB是平行四边形时,BM=CN,
∴15-t=2t,
解得:t=5秒,
此时CN=5×2=10,
过点B作BD⊥OC于D,则四边形OABD是矩形,
∴OD=AB=15,BD=OA=8,
CD=OC-OD=21-15=6,
在Rt△BCD中,BC=![]() =10,
=10,
∴BC=CN,
∴平行四边形MNCB是菱形,
故,存在t=5秒时,四边形MNCB能否为菱形.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案