题目内容
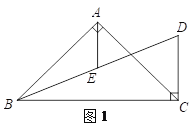
【题目】在△ABC中,AB=AC,CD⊥BC于点C,交∠ABC的平分线于点D,AE平分∠BAC交BD于点E,过点E作EF∥BC交AC于点F,连接DF.
(1)补全图1;
(2)如图1,当∠BAC=90°时,
①求证:BE=DE;
②写出判断DF与AB的位置关系的思路(不用写出证明过程);
(3)如图2,当∠BAC=α时,直接写出α,DF,AE的关系.
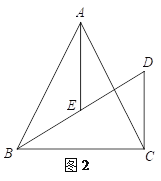
【答案】(1)答案见解析(2)证明见解析(3)![]()
【解析】分析:(1)按要求作图即可;
(2)①延长AE,交BC于点H,由等腰三角形三线合一的性质得出AH⊥BC且BH=HC.然后利用平行线分线段成比例定理即可证明结论;
②延长FE,交AB于点G,利用等腰三角形的性质证得GE=EF,再证△BEG≌△DEF即可得出DF与AB的位置关系;
(3)利用锐角三角形即可得出答案.
详解:(1)补全图1;
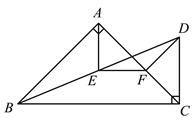
(2)①延长AE,交BC于点H.
∵AB=AC, AE平分∠BAC,
∴AH⊥BC于H,BH=HC.
∵CD⊥BC于点C,
∴EH∥CD.
∴BE=DE.
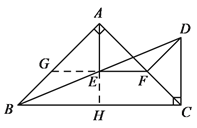
②延长FE,交AB于点G.
由AB=AC,得∠ABC=∠ACB.
由EF∥BC,得∠AGF=∠AFG.
得AG=AF.
由等腰三角形三线合一得GE=EF.
由∠GEB=∠FED,可证△BEG≌△DEF.
可得∠ABE=∠FDE.
从而可证得DF∥AB.
(3)如图所示,
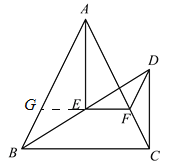
由DF∥AB且GE=EF,
![]() ≌
≌![]() ,
,
∴BG=DF,
由EF∥BC,BD平分∠ABC,
可证![]() 是等腰三角形,
是等腰三角形,
∴BG=GF,
∵![]() ,
,
∴![]() .
.

练习册系列答案
相关题目