Question

【题目】已知一次函数的图象经过点A（2，1），B（﹣1，﹣3）．

（1）求此一次函数的解析式；

（2）求此一次函数的图象与x轴、y轴的交点坐标；

（3）求此一次函数的图象与两坐标轴所围成的三角形面积．

Answer 1

【答案】（1）y=x﹣．（2）与x轴的交点坐标（，0），与y轴的交点坐标（0，﹣）．（3）．

【解析】

试题分析：根据一次函数解析式的特点，可得出方程组，得到解析式；

再根据解析式求出一次函数的图象与x轴、y轴的交点坐标；

然后求出一次函数的图象与两坐标轴所围成的三角形面积．

解：（1）根据一次函数解析式的特点，

可得出方程组，

解得，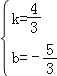

则得到y=x﹣．

（2）根据一次函数的解析式y=x﹣，

得到当y=0，x=；

当x=0时，y=﹣．

所以与x轴的交点坐标（，0），与y轴的交点坐标（0，﹣）．

（3）在y=x﹣中，

令x=0，解得：y=，

则函数与y轴的交点是（0，﹣）．

在y=x﹣中，

令y=0，解得：x=．

因而此一次函数的图象与两坐标轴所围成的三角形面积是：×=．