题目内容
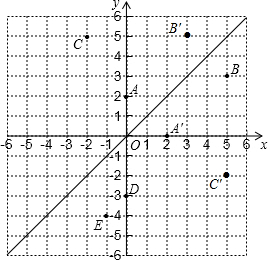
如图,在平面直角坐标系中,函数y=x的图象l是第一、三象限的角平分线.
(1)实验与探究:由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′______、C′______;
(2)归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线l的对称点P′的坐标为______;
(3)类比与猜想:坐标平面内任一点P(m,n)关于第二、四象限的角平分线的对称点P′的坐标为______;
(4)运用与拓广:已知两点D(0,-3)、E(-1,-4),试在第一、三象限的角平分线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.

(1)实验与探究:由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(-2,5)关于直线l的对称点B′、C′的位置,并写出它们的坐标:B′______、C′______;
(2)归纳与发现:结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(m,n)关于第一、三象限的角平分线l的对称点P′的坐标为______;
(3)类比与猜想:坐标平面内任一点P(m,n)关于第二、四象限的角平分线的对称点P′的坐标为______;
(4)运用与拓广:已知两点D(0,-3)、E(-1,-4),试在第一、三象限的角平分线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.

(1)∵A(0,2)关于直线l的对称点A′的坐标为(2,0),
∴B(5,3)、C(-2,5)关于直线l的对称点B′(3,5),C′(5,-2),
故答案为:(3,5);(5,-2)
(2)∵A(0,2)关于直线l的对称点A′的坐标为(2,0),
∴关于直线l对称的点的坐标横纵坐标互为相反数,
∴点P(m,n)关于第一、三象限的角平分线l的对称点P′的坐标为(n,m).
故答案为:(n,m);
(3)猜想:坐标平面内任一点P(m,n)关于第二、四象限的角平分线的对称点P′的坐标为:(-n,-m),
故答案为::(-n,-m);
(4)∵点D关于直线y=x的对称点D′(-3,0),
设过点D′E的直线解析式为y=kx+b(k≠0),
∵D′(-3,0),E(-1,-4),
∴
,解得
,
∴直线D′E的解析式为y=-2x-6,
∵点Q是直线D′E与直线y=x相交与点Q,
∴
,解得
,
∴Q(-2,-2)
∴B(5,3)、C(-2,5)关于直线l的对称点B′(3,5),C′(5,-2),
故答案为:(3,5);(5,-2)
(2)∵A(0,2)关于直线l的对称点A′的坐标为(2,0),
∴关于直线l对称的点的坐标横纵坐标互为相反数,
∴点P(m,n)关于第一、三象限的角平分线l的对称点P′的坐标为(n,m).
故答案为:(n,m);
(3)猜想:坐标平面内任一点P(m,n)关于第二、四象限的角平分线的对称点P′的坐标为:(-n,-m),
故答案为::(-n,-m);
(4)∵点D关于直线y=x的对称点D′(-3,0),
设过点D′E的直线解析式为y=kx+b(k≠0),
∵D′(-3,0),E(-1,-4),
∴
|
|
∴直线D′E的解析式为y=-2x-6,
∵点Q是直线D′E与直线y=x相交与点Q,
∴
|
|
∴Q(-2,-2)


练习册系列答案
相关题目
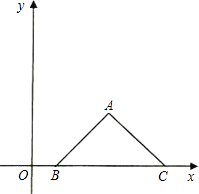 标为(3,2),B点坐标为(1,0).
标为(3,2),B点坐标为(1,0).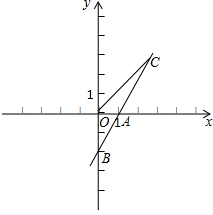

 ,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S.
,0),以CD为一边在x轴上方作矩形CDEF,且CF:CD=1:2.设矩形CDEF与△ABO重叠部分的面积为S. 回答下列问题:
回答下列问题: