题目内容
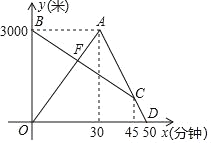
【题目】某个周末,小丽从家去园博园参观,同时妈妈参观结束从园博园回家,小丽刚到园博园就发现要下雨,于是立即按原路返回,追上妈妈后,两人一同回家(小丽和妈妈始终在同一条笔直的公路上行走)如图是两人离家的距离y(米)与小丽出发的时间x(分)之间的函数图象,请根据图象信息回答下列问题:
(1)求线段BC的解析式;
(2)求点F的坐标,并说明其实际意义;
(3)与按原速度回家相比,妈妈提前了几分钟到家?并直接写出小丽与妈妈何时相距800米.
【答案】(1)y=﹣50x+3000;(2)点F的坐标为(20,2000),其实际意义为:小丽出发20分钟时,在离家2000米处与妈妈相遇;(3)妈妈提前了10分钟到家,小丽与妈妈相距800米的时间是![]() 分钟,
分钟,![]() 分钟和37分钟.
分钟和37分钟.
【解析】
(1)由图象可知,点A(30,3000),点D(50,0),用待定系数法求出AD的解析式,再将C点横坐标代入即可求得点C的纵坐标,再由点B(0,3000),同样可由待定系数法求得BC的解析式;
(2)待定系数法求出OA的解析式,然后将其与BC的解析式联立,可求得点F的坐标,进而得其实际意义;
(3)求出直线BC与x轴交点的横坐标,再与x等于50相比较即可得妈妈提前回家的时间;小丽与妈妈相距800米有三种可能,分别求出即可.
解:(1)由图象可知,点A(30,3000),点D(50,0)
设线段AD的解析式为:y=kx+b,将点A,点D坐标代入得![]() ,
,
解得![]() ,
,
∴y=﹣150x+7500.
将x=45代入上式得y=750,
∴点C坐标为(45,750).
设线段BC的解析式为y=mx+n,将(0,3000)和(45,750)代入得:
![]() ,解得
,解得![]() ,
,
∴y=﹣50x+3000.
答:线段BC的解析式为y=﹣50x+3000.
(2)设OA的解析式为y=px,将点A(30,3000)代入得:3000=30p,
∴p=100,
∴y=100x.
由![]() 解得
解得![]() ,
,
∴点F的坐标为(20,2000),其实际意义为:小丽出发20分钟时,在离家2000米处与妈妈相遇.
(3)在y=﹣50x+3000中,令y=0得:0=﹣50x+3000,
∴x=60,
60﹣50=10,
∴妈妈提前了10分钟到家.
由|100x﹣(﹣50x+3000)|=800,得:x=![]() 或x=
或x=![]() ;
;
由(﹣150x+7500)﹣(﹣50x+3000)=800,得x=37.
答:妈妈提前了10分钟到家,小丽与妈妈相距800米的时间是![]() 分钟,
分钟,![]() 分钟和37分钟.
分钟和37分钟.

 习题精选系列答案
习题精选系列答案