��Ŀ����
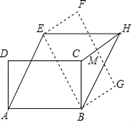
����Ŀ��������ij��ѧ�Բ���ѧ����ʳƷ��ȫ֪ʶ���˽�̶ȣ����������������ķ�ʽ���������ռ�������Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ.�������ͳ��ͼ�����ṩ����Ϣ����������⣺
��1�������ʾ������ѧ������_____�ˣ�����ͳ��Χ���������˽�����������Ӧ���ε�Բ�Ľ�Ϊ______����
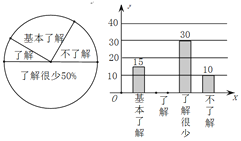
��2���벹ȫ����ͳ��ͼ��
��3��������ѧ����ѧ��900�ˣ���������������������Ƹ���ѧѧ���ж�ʳƷ��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ���������
��4���Ӷ�ʳƷ��ȫ֪ʶ�ﵽ���˽�����3��Ů����2�������������ȡ2�˲μ�ʳƷ��ȫ֪ʶ������������״ͼ���б������ǡ�ó鵽1��������1��Ů���ĸ��ʣ�
���𰸡�(1)60, 90��(2)5��(3)300�� (4) ![]()
��������
��1�������˽���������ֵ�������������ռ�İٷֱȿɵõ��������������Ȼ�����������˽���������ռ�ı�������360���õ�����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�ĽǵĶ�����
��2���ȼ�������˽������ֵ�������Ȼ��ȫ����ͳ��ͼ��
��3�����������������壬��900�������˽������������˽�����ռ�İٷֱȵĺͼ��ɣ�
��4������״ͼΪ���ֱ���A��B��ʾ����Ů������C��D��ʾ����������չʾ����12�ֵȿ��ܵĽ���������ҳ�ǡ�ó鵽1��������1��Ů���Ľ������Ȼ����ݸ��ʹ�ʽ��⣮
��1��30��50%=60��
���Խ����ʾ������ѧ������60�ˣ�
����ͳ��ͼ���������˽�����������Ӧ���ε�Բ�ĽǵĶ���Ϊ![]() ��
��
�ʴ�Ϊ60��90����
��2�����˽������ֵ�����=60-15-30-10=5��
����ͳ��ͼΪ��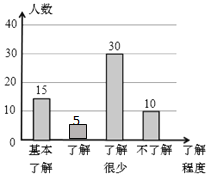 ��
��
![]()
���Թ��Ƹ���ѧѧ���ж�ʳƷ��ȫ֪ʶ�ﵽ���˽������������˽����̶ȵ�������Ϊ300�ˣ�
��4������״ͼΪ�����ֱ���A��B��ʾ����Ů������C��D��ʾ����������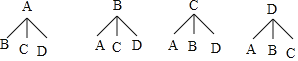
����12�ֵȿ��ܵĽ����������ǡ�ó鵽1��������1��Ů���Ľ����Ϊ8��
����ǡ�ó鵽1��������1��Ů���ĸ���= ![]() ��
��

 ��Կ���Ծ�ϵ�д�
��Կ���Ծ�ϵ�д�