Question

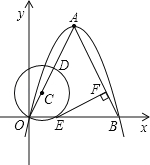
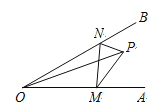
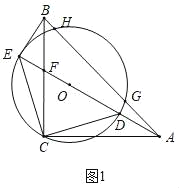
【题目】如图①，△ABC和△CDE都是等腰直角三角形，∠ACB＝∠DCE＝90°，且点A在ED的延长线上，以DE为直径的⊙O与AB交于G、H两点，连接BE．

(1)求证：BE是⊙O的切线；

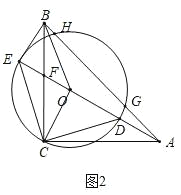
(2)如图②，连接OB、OC，若tan∠CAD＝，试判断四边形BECO的形状，请说明理由；

(3)在(2)的条件下，若BF＝，请你求出HG的长．

Answer 1

【答案】(1)证明见解析；(2)四边形BECO是平行四边形；(3)HG＝．

【解析】

(1)利用等腰直角三角形的性质，证△BCE≌△ACD，推出∠CBE＝∠CAD，证出∠AEB＝90°，即可推出结论；

(2)先证CO⊥DE，AO＝2CO，推出AD＝CO，由△BCE≌△ACD可知BE＝AD，所以BE＝CO，再证BE∥CO即可；

(3)先由平行四边形的性质推出对角线CB的长，利用三角函数求出AB的长，再在Rt△AOC中求出AO，CO的长，过点O作OM⊥AB于点M，连接OG，证△MAO∽△BAE，求出OM的长，由勾股定理求出MG的长，可进一步推出HG的长．

(1)证明：∵△ABC和△CDE都是等腰直角三角形，

∴BC＝AC，EC＝DC，

∴∠DCE＝∠ACB＝90°，

∴∠DCE﹣∠FCD＝∠ACB﹣∠FCD，

∴∠BCE＝∠ACD，

∴△BCE≌△ACD(SAS)，

∴∠CBE＝∠CAD，

∴∠ABE+∠BAE＝90°，

∴∠AEB＝90°，

∴BE⊥OE，

又∵OE是⊙O的半径，

∴BE是⊙O的切线；

(2)四边形BECO是平行四边形，

理由如下：

∵点O是ED的中点，

∴CO是DE边上的中线，

∵△CDE是等腰三角形，

∴CO是DE边上的高线，

∴CO⊥DE，

∴∠COE＝∠AOC＝90°，

∵∠AEB＝90°，

∴∠AEB＝COE，

∴CO∥BE，

∵在Rt△AOC中，tan∠CAD＝，

∴ ＝，

∴AO＝2CO，

∴DO＝CO，

∴AD＝CO，

∵△BCE≌△ACD，

∴BE＝AD，

∴BE＝CO，

∴四边形BECO是平行四边形；

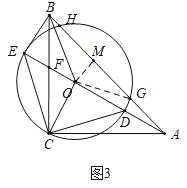
(3)∵四边形BECO是平行四边形，

∴CF＝BF＝，

∴BC＝2，

∴AC＝BC＝2，

∴AB＝ ＝2，

设OC＝x，则AO＝2x，

∵在Rt△AOC中，OC2+AO2＝AC2，

∴x2+(2x)2＝(2)2，

解得，x＝2(取正值)，

∴OC＝BE＝2，AO＝4，

如图3，过点O作OM⊥AB于点M，连接OG，

∴∠AMO＝90°，HG＝2MG，

∴∠AMO＝∠AEB＝90°，

∵∠MAO＝∠BAE，

∴△MAO∽△BAE，

∴ ，

∴ ，

∴OM＝，

在Rt△MOG中，OM2+MG2＝OG2，

∴()2+MG2＝22，

∴MG＝(取正值)，

∴HG＝2MG＝．