Question

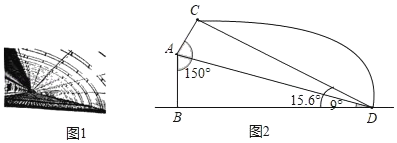
【题目】如图所示，∠AOB＝70°，以点O为圆心，以适当长为半径作弧分别交OA，OB于C，D两点；分别以C，D为圆心，以大于CD的长为半径作弧，两弧相交于点P；以O为端点作射线OP，在射线OP上取点M，连接MC、MD．若测得∠CMD＝40°，则∠MDB＝_____

Answer 1

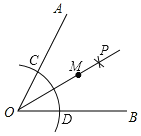
【答案】55°

【解析】

利用基本作图得到OC＝OD，OP平分∠AOB，则∠AOP＝∠BOP＝35°，再证明△OMC≌△OMD得到∠OMC＝∠OMD＝20°，然后利用三角形外角性质计算∠MDB．

解：由作法得OC＝OD，OP平分∠AOB，则∠AOP＝∠BOP＝∠AOB＝35°，

在△OMC和△OMD中

，

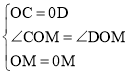∴△OMC≌△OMD（SAS），

∴∠OMC＝∠OMD＝∠CMD＝20°，

∴∠MDB＝∠DOM+∠OMD＝35°+20°＝55°．

故答案为55°．