题目内容
【题目】关于x的一元二次方程x2﹣(2k﹣1)x+k2+1＝0有两个不相等的实数根x1，x2．
(1)求实数k的取值范围；
(2)若方程的两实数根x1，x2满足|x1|+|x2|＝x1x2，求k的值．
【答案】(1)k＜﹣
；(2)-2．
【解析】
利用判别式的意义得到
，然后解不等式即可；
根据根与系数的关系得到
，
，则判断
，
，则由
得到
，所以
，然后解关于k的方程即可得到满足条件的k的值．
解：(1)根据题意得△＝(2k﹣1)2﹣4(k2+1)＞0，
解得k＜﹣；
(2)x1+x2＝2k﹣1，x1x2＝k2+1，
∵k＜﹣，
∴x1+x2＝2k﹣1＜0，
而x1x2＝k2+1＞0，
∴x1＜0，x2＜0，
∵|x1|+|x2|＝x1x2，
∴﹣(x1+x2)＝x1x2，即﹣(2k﹣1)＝k2+1，
整理得k2+2k＝0，解得k1＝0，k2＝﹣2，
而k＜﹣，
∴k＝﹣2．
练习册系列答案
阅读快车系列答案
相关题目
【题目】秋季新学期开学时，红城中学对七年级新生掌握“中学生日常行为规范”的情况进行了知识测试，测试成绩全部合格，现学校随机选取了部分学生的成绩，整理并制作成了如下不完整的图表：
分 数 段 | 频数 | 频率 |
60≤x＜70 | 9 | a |
70≤x＜80 | 36 | 0.4 |
80≤x＜90 | 27 | b |
90≤x≤100 | c | 0.2 |
请根据上述统计图表，解答下列问题：
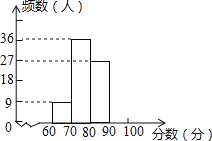
（1）在表中，a= ，b= ，c= ；
（2）补全频数直方图；
（3）根据以上选取的数据，计算七年级学生的平均成绩．
（4）如果测试成绩不低于80分者为“优秀”等次，请你估计全校七年级的800名学生中，“优秀”等次的学生约有多少人？
