题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,以点A为圆心,AC为半径,作⊙A,交AB于点D,交CA的延长线于点E,过点E作AB的平行线交⊙A于点F,连接AF,BF,DF.
(1)求证:△ABC≌△ABF;
(2)填空:
①当∠CAB= °时,四边形ADFE为菱形;
②在①的条件下,BC= cm时,四边形ADFE的面积是6![]() cm2.
cm2.

【答案】(1)证明见解析;(2)60;(3)6.
【解析】
(1)首先利用平行线的性质得到∠FAB=∠CAB,然后利用SAS证得两三角形全等即可;
(2)当∠CAB=60°时,四边形ADFE为菱形,根据∠CAB=60°,得到∠FAB=∠CAB=∠CAB=60°,从而得到EF=AD=AE,利用邻边相等的平行四边形是菱形进行判断四边形ADFE是菱形;
(3)设菱形AEFD的边长为a,易知△AEF、△AFD都是等边三角形,列出方程求出a,再在RT△ACB中,利用勾股定理即可解决问题.
(1)证明:∵EF∥AB,
∴∠E=∠CAB,∠EFA=∠FAB,
∵∠E=∠EFA,
∴∠FAB=∠CAB,
在△ABC和△ABF中,
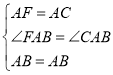 ,
,
∴△ABC≌△ABF;
(2)当∠CAB=60°时,四边形ADFE为菱形,
证明:∵∠CAB=60°,
∴∠FAB=∠CAB=∠CAB=60°,
∴EF=AD=AE,
∴四边形ADFE是菱形,
故答案为60.
(3)∵四边形AEFD是菱形,设边长为a,∠AEF=∠CAB=60°,
∴△AEF、△AFD都是等边三角形,
由题意:2×![]() a2=6
a2=6![]() ,
,
∴a2=12,
∵a>0,
∴a=2![]() ,
,
∴AC=AE=2![]() ,
,
在RT△ACB中,∠ACB=90°,AC=2![]() ,∠CAB=60°,
,∠CAB=60°,
∴∠ABC=30°,
∴AB=2AC=4![]() ,BC=
,BC=![]() =6.
=6.
故答案为6.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目