题目内容
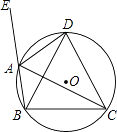
【题目】如图,△ABC和△ADE都是等腰三角形,BC、DE分别是这两个等腰三角形的底边,且∠BAC=∠DAE.
(1)求证:BD=CE;
(2)连接DC.如果CD=CE,试说明直线AD垂直平分线段BC.

【答案】(1)证明见解析;(2)说明见解析.
【解析】(1)由△ABC和△ADE都是等腰三角形且∠BAC=∠DAE知AB=AC、AD=AE、∠BAD=∠CAE,证△ABD≌△ACE即可得证;
(2)由(1)知BD=CE,结合CD=CE知CD=BD,据此可得点D在BC的中垂线上,根据AB=AC知点A在BC的中垂线上,从而得出AD垂直平分线段BC.
(1)∵△ABC和△ADE都是等腰三角形,且∠BAC=∠DAE,∴AB=AC,AD=AE,∠BAD=∠CAE.
在△ABD和△ACE中,
∵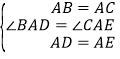 ,∴△ABD≌△ACE(SAS),∴BD=CE.
,∴△ABD≌△ACE(SAS),∴BD=CE.
(2)由(1)知△ABD≌△ACE,∴BD=CE.
∵CD=CE,∴CD=BD,∴点D在BC的中垂线上.
∵AB=AC,∴点A在BC的中垂线上,∴AD垂直平分线段BC.

练习册系列答案
相关题目