题目内容
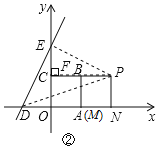
【题目】正方形OABC的边长为1,把它放在如图所示的直角坐标系中,点M(t,0)是x轴上一个动点(t≥1),连接BM,在BM的右侧作正方形BMNP;直线DE的解析式为y=2x+b,与x轴交于点D,与y轴交于点E,当△PDE为等腰直角三角形时,点P的坐标是_____.

【答案】(4,4)或(4,2).
【解析】
过点P作PF⊥BC交CB的延长线于点F,根据同角的余角相等可得∠ABM=∠FBP,然后利用“角角边”证明△ABM和△FBP全等,根据全等三角形对应边相等可得BF=AB,PF=AM,然后根据正方形OABC的边长为2以及点M(t,0)表示出点P的坐标,再利用直线DE的解析式求出点D、E的坐标,然后分①DE是斜边时,利用勾股定理以及两点间的距离公式分别表示出PD、PE、DE的平方,再根据等腰直角三角形的三边关系,②PD是斜边时,过点P作PF⊥y轴于点F,然后利用“角角边”证明△EDO和△PEF全等,根据全等三角形对应边相等可得EF=DO,PC=EO,然后用b、t表示并求解即可得到点P的坐标.
如图,

过点P作PF⊥BC交CB的延长线于点F,
∵四边形OABC与四边形BMNP都是正方形,
∴∠ABM+∠MBF=90°,
∠FBP+∠MBF=90°,
∴∠ABM=∠FBP,
在△ABM和△FBP中,
 ,
,
∴△ABM≌△FBP(AAS),
∴BF=AB,PF=AM,
∵正方形OABC的边长为1,点M(t,0),
∴BF=1,PF=t-1,
点P到x轴的距离为t-1+1=t,
∴点P的坐标为(2,t),
又∵当y=0时,2x+b=0,解得x=-![]() ,
,
当x=0时,y=b,
∴点D(-![]() ,0),E(0,b),
,0),E(0,b),
DE是斜边时,
PD2=(![]() +2)2+t2,PE2=(b-t)2+22,DE2=(
+2)2+t2,PE2=(b-t)2+22,DE2=(![]() )2+b2,
)2+b2,
∵△PDE是等腰直角三角形,
∴PD2=PE2,且PD2+PE2=DE2,
即(![]() +2)2+t2=(b-t)2+22,且(
+2)2+t2=(b-t)2+22,且(![]() +2)2+t2+(b-t)2+22=(
+2)2+t2+(b-t)2+22=(![]() )2+b2,
)2+b2,
![]() b2+2b+4+t2=b2-2bt+t2+4,且
b2+2b+4+t2=b2-2bt+t2+4,且![]() b2+2b+4+t2+b2-2bt+t2+4=
b2+2b+4+t2+b2-2bt+t2+4=![]() b2+b2,
b2+b2,
整理得,b=![]() (t+2)且t2-b(t-2)+16=0,
(t+2)且t2-b(t-2)+16=0,
∴t2-![]() (t+2)(t-2)+16=0,
(t+2)(t-2)+16=0,
整理得,t2=16,
解得t1=4,t2=-4(舍去),
∴点P的坐标是(4,4);
②PD是斜边时,∵△PDE是等腰直角三角形,
∴PE⊥DE,且PE=DE,
过点P作PF⊥y轴于点F,
∵∠DEO+∠PEO=90°,∠DEO+∠EDO=90°,
∴∠PEO=∠EDO,
在△EDO和△PEF中,
 ,
,
∴△EDO≌△PEF(AAS),
∴EF=DO=![]() ,PC=EO=b,
,PC=EO=b,
又∵点P(4,t),
∴b=4,b-t=![]() ,
,
解得t=![]() =
=![]() ×4=2,
×4=2,
∴点P坐标为(4,2),
此时点C、F重合,点M、A重合,
综上所述,点P的坐标为(4,4)或(4,2).
故答案为:(4,4)或(4,2).

 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
|
用水量(吨) |
|
|
|
|
|
费用(元) |
|
|
|
|
|
根据表格中提供的信息,回答以下问题:
![]() 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准;
![]() 若小明家
若小明家![]() 月份用水
月份用水![]() 吨,则应缴多少元?
吨,则应缴多少元?
![]() 若小明家
若小明家![]() 月份缴水费
月份缴水费![]() 元,则
元,则![]() 月份用水多少吨?
月份用水多少吨?





