题目内容
【题目】如图,四边形ABCD内接于⊙O,∠DAE是四边形ABCD的一个外角,且AD平分∠CAE.
求证:DB=DC.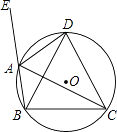
【答案】证明:∵∠DAC与∠DBC是同弧所对的圆周角,
∴∠DAC=∠DBC.
∵AD平分∠CAE,
∴∠EAD=∠DAC,
∴∠EAD=∠DBC.
∵四边形ABCD内接于⊙O,
∴∠EAD=∠BCD,
∴∠DBC=∠DCB,
∴DB=DC
【解析】先根据圆周角定理得出∠DAC=∠DBC,再由角平分线的性质得出∠EAD=∠DAC,根据圆内接四边形的性质得出∠EAD=∠BCD,由此可得出结论.
【考点精析】利用圆周角定理和圆内接四边形的性质对题目进行判断即可得到答案,需要熟知顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;把圆分成n(n≥3):1、依次连结各分点所得的多边形是这个圆的内接正n边形2、经过各分点作圆的切线,以相邻切线的交点为顶点的多边形是这个圆的外切正n边形.

 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案【题目】某商店三、四月份出售同一品牌各种规格空调销售台输入下表,回答:
|
|
|
| |
三月 |
|
|
|
|
四月 |
|
|
|
|
![]() 商店平均每月销售空调________台;
商店平均每月销售空调________台;
![]() 商店出售各种规格的空调中,众数有________匹;
商店出售各种规格的空调中,众数有________匹;
![]() 在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
在研究六月份进货时,商店经理决定________(匹)的空调要多进,________(匹)的空调要少进.
【题目】为了鼓励居民节约用水,某市自来水公司对每户月用水量进行计费,每户每月用水量在规定吨数以下的收费标准相同;规定吨数以上的超过部分收费标准相同,以下是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
|
用水量(吨) |
|
|
|
|
|
费用(元) |
|
|
|
|
|
根据表格中提供的信息,回答以下问题:
![]() 求出规定吨数和两种收费标准;
求出规定吨数和两种收费标准;
![]() 若小明家
若小明家![]() 月份用水
月份用水![]() 吨,则应缴多少元?
吨,则应缴多少元?
![]() 若小明家
若小明家![]() 月份缴水费
月份缴水费![]() 元,则
元,则![]() 月份用水多少吨?
月份用水多少吨?