题目内容
【题目】如图△ABC中,∠BAC=78°,AB=AC,P为△ABC内一点,连BP,CP,使∠PBC=9°,∠PCB=30°,连PA,则∠BAP的度数为_______.

【答案】69°
【解析】
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC,根据等边三角形的性质得到AD=AB=AC,求出∠DAC、∠ACD、∠ADC的度数,根据三角形的内角和定理求出∠ABC=∠ACB=51°,即∠CDB=141°=∠BPC,再证△BDC≌△BPC,得到PC=DC,进一步得到等边△DPC,推出△APD≌△APC,根据全等三角形的性质得到∠DAP=∠CAP=9°,即可求出答案.
在BC下方取一点D,使得三角形ABD为等边三角形,连接DP、DC
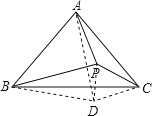
∴AD=AB=AC,![]()
![]()
∴![]()
∵![]()
∴![]()
∴![]()
又∵![]()
∴△BDC≌△BPC,
∴PC=DC,
又∵![]()
∴△DPC是等边三角形,
∴△APD≌△APC,
∴![]()
∴![]()
故答案为:69°.

练习册系列答案
相关题目