题目内容
【题目】如下表，从左边第1个格子开始依次在每个格子中填入一个正整数，第1个格子填入
，第2个格子填入
，第3个格子填入
，…，第n个格子填入
，以此类推. 表中任意4个相邻格子中所填正整数之和都相等，其中
．
|
|
|
| … |
| … |
（1）若
，求
；
；
（2）将表中前2020个数的和记为S，若
，求S的值．
【答案】（1）
=1，
=5；（2）S=9090.
【解析】
（1）根据“任意四个相邻格子中所填正整数之和都相等”可知此表是由四个整数重复排列而成，即可求出a5和a2019
（2）由于是四个数重复出现，因此可用前四个数的重复多次计算出结果，根据题意找出等量关系，求出前四个格子之和，即可求出S
（1）由题意可知a1+a2+a3+a4= a2+a3+a4+a5
∴a5=a1=1
∵任意4个相邻格子中所填正整数之和都相等,可知此表是由四个整数重复排列而成
∴
=a3=5；
故本题答案为：a5=1，a2019=5
（2）
∴
∵
∴
∵任意4个相邻格子中所填正整数之和都相等．
∴前2020个数的和
.
又
∴
.
同理
.
∴
.
练习册系列答案
相关题目
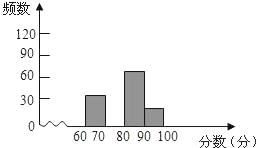
【题目】为迎接国庆60周年，某校举行以“祖国成长我成长”为主题的图片制作比赛，赛后整理参赛同学的成绩，并制作成图表如下：
分数段 | 频数 | 频率 |
60≤x＜70 | 30 | 0.15 |
70≤x＜80 | m | 0.45 |
80≤x＜90 | 60 | n |
90≤x＜100 | 20 | 0.1 |
请根据以上图表提供的信息，解答下列问题：
（1）表中m和n所表示的数分别为：m= ，n= ；
（2）请在图中，补全频数分布直方图；
（3）比赛成绩的中位数落在哪个分数段；
（4）如果比赛成绩80分以上（含80分）可以获得奖励，那么获奖率是多少？
