Question

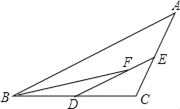
【题目】在△ABC中，D、E分别是BC、AC中点，BF平分∠ABC．交DE于点F．AB＝8，BC＝6，则EF的长为(　　)

A. 1B. 2C. 3D. 4

Answer 1

【答案】A

【解析】

利用中位线定理，得到DE∥AB，根据平行线的性质，可得∠EDC=∠ABC，再利用角平分线的性质和三角形内角外角的关系，得到DF=DB，进而求出DF的长，易求EF的长度．

∵在△ABC中，D、E分别是BC、AC的中点，AB=8，

∴DE∥AB，DE=AB=4．

∴∠EDC=∠ABC．

∵BF平分∠ABC，

∴∠EDC=2∠FBD．

∵在△BDF中，∠EDC=∠FBD+∠BFD，

∴∠DBF=∠DFB，

∴FD=BD=BC=×6=3．

∴FE=DE-DF=4-3=1．

故选A．