题目内容
【题目】现从A,B向甲、乙两地运送蔬菜,A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨.
(1)设A地到甲地运送蔬菜x吨,请完成下表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | |
B |
(2)设总运费为W元,请写出W与x的函数关系式
(3)怎样调运蔬菜才能使运费最少?
【答案】(1)见解析(2)W=5x+1275(3)当x最小为1时,W有最小值 1280元
【解析】解:(1)完成填表:
运往甲地(单位:吨) | 运往乙地(单位:吨) | |
A | x | 14﹣x |
B | 15﹣x | x﹣1 |
(2)W=50x+30(14-x)+60(15-x)+45(x-1),
整理得,W=5x+1275。
(3)∵A,B到两地运送的蔬菜为非负数,
∴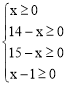 ,解不等式组,得:1≤x≤14。
,解不等式组,得:1≤x≤14。
在W=5x+1275中,W随x增大而增大,
∴当x最小为1时,W有最小值 1280元。
(1)根据题意A,B两个蔬菜市场各有蔬菜14吨,其中甲地需要蔬菜15吨,乙地需要蔬菜13吨,可得解。
(2)根据从A到甲地运费50元/吨,到乙地30元/吨;从B地到甲运费60元/吨,到乙地45元/吨可列出总费用,从而可得出答案。
(3)求出x的取值范围,利用w与x之间的函数关系式,求出函数最值即可。

【题目】某市篮球队到市一中选拔一名队员.教练对王亮和李刚两名同学进行5次3分球投篮测试,每人每次投10个球,图记录的是这两名同学5次投篮所投中的个数.

(1)请你根据图中的数据,填写下表;
姓名 | 平均数 | 众数 | 方差 |
王亮 | 7 | ||
李刚 | 7 | 2.8 |
(2)你认为谁的成绩比较稳定,为什么?
(3)若你是教练,你打算选谁?简要说明理由.
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?