��Ŀ����
����Ŀ��ij�������Ƴ�һ���ɱ���λ500Ԫ/�˵�ʡ��������·���ο�����y����/�£������α���x��Ԫ/�ˣ�֮��Ĺ�ϵΪy=��x+1300����֪���������ܲ��Ź涨��������·������800Ԫ/�ˡ�1200Ԫ/��֮�䣮
��1��Ҫ����������·ÿ���ο�����������200�����ڣ����������·���۵�ȡֵ��Χ��
��2����Ӫ����������·ÿ������Ҫ����ͳɱ���
��3��������������·�����α���Ϊ����ʱ���ɻ�����������������Ƕ��٣�
���𰸡���1��ȡֵ��ΧΪ1100Ԫ/�ˡ�1200Ԫ/��֮�䣻��2��50000����3��x=900ʱ��w���=160000
�������������������1�����������в���ʽ���ɣ�
��2�����ݱ��ۼ�ȥ�ɱ��ɵõ������Ľ���ʽ������һ�κ�����ͼ����⼴�ɣ�
��3��������������˴γ��Լ۸ɵõ������Ľ���ʽ��Ȼ����ݶ��κ�������ֵ��⼴��.
�����������1�����������![]() ʱ����
ʱ����![]() ��
��
����![]()
��Ҫ����������·ÿ���ο�����������200�����ڣ���������·���۵�ȡֵ��ΧΪ1100Ԫ/��~1200Ԫ/��֮�䣻
��2��![]() ��
��![]() ����
����![]()
��![]() ���൱
���൱![]() ʱ��z��ͣ���
ʱ��z��ͣ���![]() ��
��
��3������![]()
��![]() ʱ��
ʱ��![]() .
.
�����͡������
��������
23
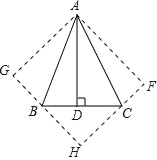
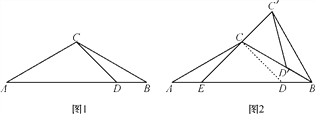
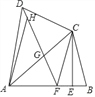
����Ŀ����֪�ı���ABCD�У�AB=AD���Խ���ACƽ�֡�DAB������C��CE��AB�ڵ�E����FΪAB��һ�㣬��EF=EB������DF��
��1����֤��CD=CF��
��2������DF����AC�ڵ�G����֤����DGC����ADC��
��3������HΪ�߶�DG��һ�㣬����AH������ADC=2��HAG��AD=3��DC=2����![]() ��ֵ��
��ֵ��
���𰸡���1��֤������������2��֤������������3��![]() ��
��
�������������������1�������DAC=��BAC������ȫ�������ε��ж��ó���ADC�ա�ABC������ȫ�������ε����ʵó�CD=CB���ɣ�
��2������ȫ�������ε����ʵó���ADC=��B�������ADC+��AFC=180������DCF+��DAF=180���������CDG=��DAC���������������ε����ʵó����ɣ�
��3���������������ε����ʵó���DGC=��ADC�� ![]() �������HAG=��AHG��
�������HAG=��AHG�� ![]() ���������������ε��ж��ó���DGC����AGF���������������ε����ʵó����ɣ�
���������������ε��ж��ó���DGC����AGF���������������ε����ʵó����ɣ�
�����������1��֤������ACƽ�֡�DAB��
���DAC=��BAC��
����ADC����ABC��
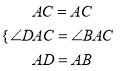
���ADC�ա�ABC��
��CD=CB��
��CE��AB��EF=EB��
��CF=CB��
��CD=CF��
��2���ߡ�ADC�ա�ABC��
���ADC=��B��
��CF=CB��
���CFB=��B��
���ADC=��CFB��
���ADC+��AFC=180����
���ı���AFCD���ڽǺ͵���360����
���DCF+��DAF=180����
��CD=CF��
���CDG=��CFD��
�ߡ�DCF+��CDF+��CFD=180����
���DAF=��CDF+��CFD=2��CDG��
�ߡ�DAB=2��DAC��
���CDG=��DAC��
�ߡ�DCG=��ACD��
���DGC�ס�ADC��
��3���ߡ�DGC�ס�ADC��
���DGC=��ADC�� ![]() ��
��
�ߡ�ADC=2��HAG��AD=3��DC=2��
���HAG=![]() ��DGC��
��DGC�� ![]() ��
��
���HAG=��AHG�� ![]() ��
��
��HG=AG��
�ߡ�GDC=��DAC=��FAG����DGC=��AGF��
���DGC����AGF��
��![]() ��
��
��![]() ��
��

 �żӾ���ϵ�д�
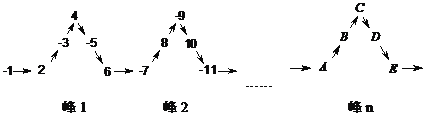
�żӾ���ϵ�д�����Ŀ�����±�������ߵ�1�����ӿ�ʼ������ÿ������������һ������������1����������![]() ����2����������
����2����������![]() ����3����������
����3����������![]() ��������n����������
��������n����������![]() ���Դ�����. ��������4�����ڸ���������������֮�Ͷ���ȣ�����
���Դ�����. ��������4�����ڸ���������������֮�Ͷ���ȣ�����![]() ��
��
|
|
|
| �� |
| �� |
��1����![]() ����
����![]() ��
��![]() ��
��
��2��������ǰ2020�����ĺͼ�ΪS����![]() ����S��ֵ��
����S��ֵ��
����Ŀ��Ϊ�˼�ǿ����Ľ�ˮ��ʶ,��������ˮ��Դ�����в��ü۸���ص��ֶδﵽ��ˮ��Ŀ�ģ���������ˮ�շѵļ�Ŀ�����±���
��Ŀ�� | |
ÿ����ˮ�� | ���� |
������6m3�IJ��� | 3Ԫ/m3 |
����6m3������10m3�IJ��� | 5Ԫ/m3 |
����10m3�IJ��� | 9Ԫ/m3 |
ע��ˮ�Ѱ��½��� | |
�������������ݽ���������⣺
(1)��գ����û�����2�·���ˮ4m3����Ӧ��ˮ��_______Ԫ��
(2)���û�����3�·���ˮam3(����6m3<a<10m3)����Ӧ��ˮ�Ѷ���Ԫ?(�ú�a�Ĵ���ʽ��ʾ��������)
(3)���û�����4��5�����¹���ˮ15m3(5�·���ˮ��������4�·�),��4�·���ˮxm3����û�����4��5�����¹���ˮ�Ѷ���Ԫ?(�ú�x�Ĵ���ʽ��ʾ��������)