题目内容
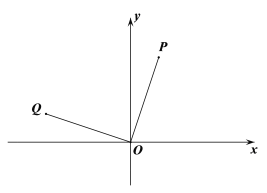
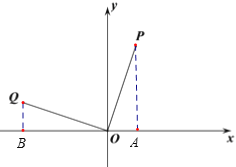
【题目】如图所示,点P的坐标为(1,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
(1)写出点Q的坐标是________;
(2)若把点Q向右平移![]() 个单位长度,向下平移
个单位长度,向下平移![]() 个单位长度后,得到的点
个单位长度后,得到的点![]() 落在第四象限,求
落在第四象限,求![]() 的取值范围;
的取值范围;
(3)在(2)条件下,当![]() 取何值,代数式
取何值,代数式![]() 取得最小值.
取得最小值.
【答案】(1)Q(-3,1)(2)a>3(3)0
【解析】
(1)如图,作PA⊥x轴于A,QB⊥x轴于B,则∠PAO=∠OBQ=90°,证明△OBQ≌△PAO(AAS),从而可得OB=PA,QB=OA,继而根据点P的坐标即可求得答案;
(2)利用点平移的规律表示出Q′点的坐标,然后根据第四象限点的坐标特征得到a的不等式组,再解不等式即可;
(3)由(2)得,m=-3+a,n=1-a,代入所求式子得![]()
![]() ,继而根据偶次方的非负性即可求得答案 .
,继而根据偶次方的非负性即可求得答案 .
(1)如图,作PM⊥x轴于A,QN⊥x轴于B,则∠PAO=∠OBQ=90°,
∴∠P+∠POA=90°,
由旋转的性质得:∠POQ=90°,OQ=OP,
∴∠QOB+∠POA=90°,
∴∠QOB=∠P,
∴△OBQ≌△PAO(AAS),
∴OB=PA,QB=OA,
∵点P的坐标为(1,3),
∴OB=PA=3,QB=OA=1,
∴点Q的坐标为(-3,1);
(2)把点Q(-3,1)向右平移a个单位长度,向下平移a个单位长度后,
得到的点M的坐标为(-3+a,1-a),
而M在第四象限,
所以![]() ,
,
解得a>3,
即a的范围为a>3;
(3)由(2)得,m=-3+a,n=1-a,
∴![]()
![]()
![]()
![]() ,
,
∵![]() ,
,
∴当a=4时,代数式![]() 的最小值为0.
的最小值为0.

练习册系列答案
相关题目