题目内容
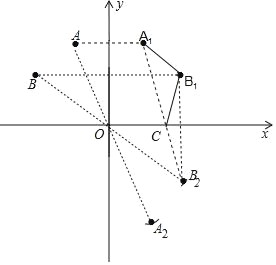
【题目】如图,已知:在直角坐标系中,A(﹣2,4)B(﹣4,2);A1、B1是A、B关于y轴的对称点;
(1)请在图中画出A、B关于原点O的对称点A2,B2(保留痕迹,不写作法);并直接写出A1、A2、B1、B2的坐标.
(2)试问:在x轴上是否存在一点C,使△A1B1C的周长最小,若存在求C点的坐标,若不存在说明理由.

【答案】(1)点A1、A2、B1、B2的坐标分别为(2,4),(4,2),(2,﹣4),(4,﹣2);(2)存在.![]()
【解析】
(1)如图,分别延长AO和BO,使A2O=AO,B2O=BO,从而得到点A2,B2,然后利用关于y轴对称和原点对称的点的坐标特征写出点A1、A2、B1、B2的坐标;
(2)连接A1B2交x轴于C,如图,利用点B1与B2关于x轴对称得到CB1=CB2,利用两点之间线段最短得到此时CA1+CB1的值最小,所以△A1B1C的周长最小,接着利用待定系数法求出直线A1B2的解析式为y=3x+10,然后求出直线与x轴的交点坐标即可.
解:(1)如图,点A2,B2为所作,点A1、A2、B1、B2的坐标分别为(2,4),(4,2),(2,﹣4),(4,﹣2);
(2)存在.
连接A1B2交x轴于C,如图,
∵点B1与B2关于x轴对称,
∴CB1=CB2,
∴CA1+CB1=CA1+CB2=A1B2,
此时CA1+CB1的值最小,则△A1B1C的周长最小,
设直线A1B2的解析式为y=kx+b,
把A1(2,4),B2(4,﹣2)代入得![]() ,解得
,解得![]() ,
,
∴直线A1B2的解析式为y=﹣3x+10,
当y=0时,﹣3x+10=0,解得x=![]() ,
,
∴C点坐标为(![]() ,0).
,0).

练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目