题目内容
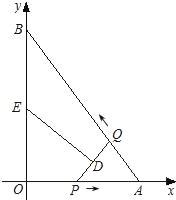
【题目】已知数轴上,一动点Q从原点O出发,沿数轴以每秒2个单位长度的速度来回移动,其移动的方式是:先向右移动1个单位长度,再向左移动2个单位长度,又向右移动3个单位长度,再向左移动4个单位长度,又向右移动5个单位长度…,
![]()
(1)动点Q运动3秒时,求此时Q在数轴上表示的数?
(2)当动点Q第一次运动到数轴上对应的数为10时,求Q运动的时间t;
(3)若5秒时,动点Q激活所在位置P点,P点立即以0.1个单位长度/秒的速度沿数轴运动,试求点P激活后第一次与继续运动的点Q相遇时所在的位置.
【答案】(1)此时Q在数轴上表示的数是2;(2)Q运动的时间为95秒;(3)点P激活后第一次与继续运动的点Q相遇时所在的位置是![]() 或
或![]() .
.
【解析】
(1)根据动点Q的移动规律,分析得出0.5秒和3秒时所在位置,即可求出答案;
(2)分析动点Q的移动规律,求出到达数轴上表示数10的位置时所走的总路程,然后根据时间=路程÷速度进行计算即可;
(3)首先求出5秒时,动点Q所在位置为2,然后分情况讨论:①P点向左运动,②P点向右运动,分别列出方程求出相遇时用的时间,然后再计算点Q相遇时所在的位置即可.
解:(1)由题意得:0.5秒动点Q所在的位置为1,1.5秒动点Q所在的位置为1,
∴3秒时动点Q所在的位置为2,即此时Q在数轴上表示的数是2;
(2)设每改变一次方向为一次运动,
分析动点Q的移动规律可知,第一次到达数轴上表示数1的位置,第3次到达数轴上表示数2的位置,第5次到达数轴上表示数3的位置,…,
所以第2n-1次到达数n的位置,
所以第19次到达数轴上表示数10的位置,
此时运动的总路程为:![]() ,
,
∴Q运动的时间t=190÷2=95秒;
(3)∵3秒时,动点Q所在的位置为2,
∴5秒时,动点Q所在位置为2,
①若P点向左运动,动点Q先向右运动5个单位长度到数轴3的位置,再向左运动6个单位长度,
Q在数轴3位置向左运动时,PQ=5+![]() ×0.1=
×0.1=![]() ,
,
设点P激活后第一次与继续运动的点Q相遇时用的时间为t1,则(20.1)t1=![]() ,
,
解得:t1=![]() ,
,
∴点P激活后第一次与继续运动的点Q相遇时所在的位置为:(2+![]() ×0.1+
×0.1+![]() ×0.1)=
×0.1)=![]() ;
;
②若P点向右运动,动点Q先向右运动5个单位长度到数轴3的位置,再向左运动6个单位长度,
Q在数轴3位置向左运动时,PQ=5![]() ×0.1=
×0.1=![]() ,
,
设点P激活后第一次与继续运动的点Q相遇时用的时间为t2,则(2+0.1)t2=![]() ,
,
解得:t2=![]() ,
,
∴点P激活后第一次与继续运动的点Q相遇时所在的位置为:(2![]() ×0.1
×0.1![]() ×0.1)=
×0.1)=![]() ;
;
综上所述,点P激活后第一次与继续运动的点Q相遇时所在的位置是![]() 或
或![]() .
.

【题目】据某市交通运管部门![]() 月份的最新数据,目前该市市面上的共享单车数量已达
月份的最新数据,目前该市市面上的共享单车数量已达![]() 万辆,共享单车也逐渐成为高校学生喜爱的“绿色出行”方式之一.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
万辆,共享单车也逐渐成为高校学生喜爱的“绿色出行”方式之一.某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.
使用次数 |
|
|
|
|
|
人数 |
|
|
|
|
|
(1)求这天部分出行学生使用共享单车次数的平均数,中位数和众数.
(2)若该校这天有![]() 名学生出行,估计使用共享单车次数在
名学生出行,估计使用共享单车次数在![]() 次以上(含
次以上(含![]() 次)的学生数.
次)的学生数.