题目内容
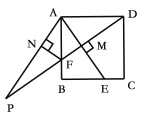
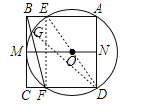
【题目】如图,![]() 过正方形
过正方形![]() 的顶点
的顶点![]() ,且与
,且与![]() 相切于点
相切于点![]() 分别交
分别交![]() 于
于![]() 两点,连接
两点,连接![]() 并延长交
并延长交![]() 于点
于点![]() .
.
(1)求证![]()
(2)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() 求
求![]() 的长.
的长.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
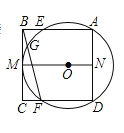
(1)根据⊙O与BC相切于点M,可得∠BMN=90°,得四边形ABCD是正方形,再根据垂径定理即可证明AN=DN;
(2)解法一:接DE,EF,DG,可得DE是⊙O的直径,且四边形AEFD是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,然后由∠BFE=∠EDG,得sin∠BFE=sin∠EDG,进而可得EG的长;
解法二:连接![]() 由圆周角定理可得
由圆周角定理可得![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,由圆内接四边形性质求得
是矩形,由(1)知四边形ABMN是矩形,设OA=r,则ON=8-r,AN=4,在Rt△AON中,根据勾股定理可得r的值,由圆内接四边形性质求得![]() ,从而利用AA定理求得
,从而利用AA定理求得![]() ,从而利用相似三角形的性质列比例式求解即可.
,从而利用相似三角形的性质列比例式求解即可.
解:![]()
![]() 与边
与边![]() 相切与点,
相切与点,![]()
![]() 四边形
四边形![]() 是正方形,
是正方形,
![]()
![]()
由垂径定理得![]()
![]() 解法一:连接
解法一:连接![]()
![]()
![]() ,
,
![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形.
是矩形.
由![]() 知四边形
知四边形![]() 是矩形,
是矩形,
![]()
设![]() ,在
,在![]() 中
中
由勾股定理得![]() ,解得
,解得![]()
![]() ,
,
![]()
![]() ,
,![]()
![]()
![]()
![]()
即![]()
![]()
解法二:连接![]()
![]()
![]()
![]() 是
是![]() 的直径,且四边形
的直径,且四边形![]() 是矩形,
是矩形,
由![]() 知四边形
知四边形![]() 是矩形,
是矩形,
![]()
设![]() ,在
,在![]() 中,
中,
由勾股定理得![]() ,解得
,解得![]()
![]()
![]()
![]()
![]()
![]()
![]()
即![]()
![]() .
.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目