题目内容
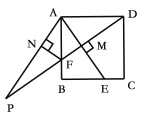
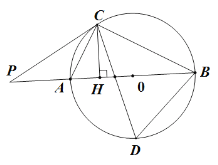
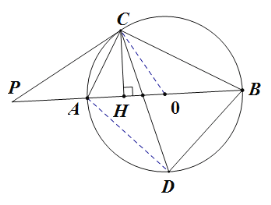
【题目】如图,AB是△ABC外接圆的直径,O为圆心,CHAB,垂足为H,且∠PCA=∠ACH, CD平分∠ACB,交⊙O于点D,连接BD,AP=2.
(1)判断直线PC是否为⊙O的切线,并说明理由;
(2)若∠P=30°,求AC、BC、BD的长.
(3)若tan∠ACP=![]() ,求⊙O半径.
,求⊙O半径.
【答案】(1)PC 是⊙O的切线,理由见解析;(2)AC=2;BC=![]() ;BD=
;BD=![]() ;(3)⊙O的半径为3.
;(3)⊙O的半径为3.
【解析】
(1)连接OC,根据等腰三角形的性质及垂直的定义得到∠PCA+∠OCA=90°,即可证明PC 是⊙O的切线;
(2)根据∠P=30°,可求得∠AOC=60°,进而得到∠OAC=60°,求出∠PCA=30°,AC=AP=2,利用∠ABC=![]() ∠AOC=30°,求出AB=2AC=4,利用勾股定理求出BC,利用垂径定理得到AD=BD,利用等腰直角三角形的性质即可求出BD的长;
∠AOC=30°,求出AB=2AC=4,利用勾股定理求出BC,利用垂径定理得到AD=BD,利用等腰直角三角形的性质即可求出BD的长;
(3)根据直径和切线的性质得到∠ABC=∠ACH,由tan∠ABC=tan∠ACP=![]() 得到
得到![]() ,再证明△PAC∽△PCB,得到
,再证明△PAC∽△PCB,得到![]() ,求出PC,再求出PB,故可求出半径的长.
,求出PC,再求出PB,故可求出半径的长.
(1)PC 是⊙O的切线
理由:连接OC,
![]() OA=OC
OA=OC
![]() ∠OCA=∠OAC
∠OCA=∠OAC
![]() CHAB
CHAB
![]() ∠ACH+∠OAC=90°
∠ACH+∠OAC=90°
![]() ∠PCA=∠ACH
∠PCA=∠ACH
![]() ∠PCA+∠OAC=90°
∠PCA+∠OAC=90°
即:∠PCA+∠OCA=90°
![]() OC为⊙O的半径
OC为⊙O的半径
![]() PC 是⊙O的切线
PC 是⊙O的切线
(2)连接AD,
![]() PC 是⊙O的切线
PC 是⊙O的切线
![]() ∠PCO=90°
∠PCO=90°
![]() ∠P=30°
∠P=30°
![]() ∠AOC=60°
∠AOC=60°
![]() OA=OC
OA=OC
![]() ∠OAC=60°
∠OAC=60°
∴∠ACP=∠OAC-∠P=30°
![]() AC=AP=2
AC=AP=2
![]() ∠ABC=
∠ABC=![]() ∠AOC=
∠AOC=![]() 60°=30°
60°=30°
![]() AB=2AC=
AB=2AC=![]()
![]()
![]()
![]() CD平分∠ACB
CD平分∠ACB
![]() ∠ACD=∠BCD
∠ACD=∠BCD
![]() 弧AD与弧BD相等,
弧AD与弧BD相等,
![]() AD=BD
AD=BD
![]() AB为⊙O的直径
AB为⊙O的直径
![]() ∠ADB=90°
∠ADB=90°
∴△ABD是等腰直角三角形;
![]()
![]() ;
;
(3)![]() AB为⊙O的直径,
AB为⊙O的直径,
![]() ∠ACB=90°
∠ACB=90°
![]() ∠ACH+∠BCH=90°
∠ACH+∠BCH=90°
![]() CHAB
CHAB
![]() ∠B+∠BCH=90°
∠B+∠BCH=90°
![]() ∠ABC=∠ACH
∠ABC=∠ACH
![]() tan∠ABC=tan∠ACP=
tan∠ABC=tan∠ACP=![]()
![]()
![]()
![]() ∠PCA=∠ACH
∠PCA=∠ACH
![]() ∠PCA=∠ABC
∠PCA=∠ABC
![]() ∠P=∠P
∠P=∠P
![]() △PAC∽△PCB
△PAC∽△PCB
![]()
![]()
![]() AP=2
AP=2
![]() PC=4
PC=4
![]() PB=8
PB=8
![]() AB=6
AB=6
![]() ⊙O的半径为3.
⊙O的半径为3.