题目内容
【题目】如图,AB是⊙O的直径,PC切⊙O于点C,AB的延长线与PC交于点P,PC的延长线与AD交于点D,AC平分∠DAB. 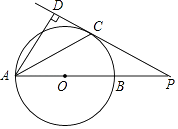
(1)求证:AD⊥PC;
(2)连接BC,如果∠ABC=60°,BC=2,求线段PC的长. 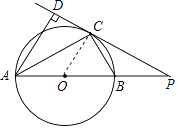
【答案】
(1)解:连接OC,∵AC平分∠DAB,
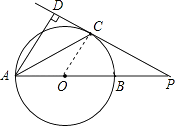
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠ACO,
∴AD∥OC,
∵PC切⊙O于点C,
∴OC⊥PC,
∴AD⊥PC;
(2)解:∵∠ABC=60°,OC=OB,
∴△BOC是等边三角形,
∴OC=2,
∴∠COP=60°,
∵PC切⊙O于点C,
∴∠OCP=90°,
∴PC=2 ![]() .
.
【解析】(1)连接OC,根据角平分线的定义得到∠DAC=∠BAC,根据等腰三角形的性质得到∠OAC=∠ACO,推出AD∥OC,于是得到结论;(2)根据已知条件得到△BOC是等边三角形,解直角三角形即可得到结论.
【考点精析】根据题目的已知条件,利用切线的性质定理的相关知识可以得到问题的答案,需要掌握切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案【题目】甲、乙两组同学进行一分钟引体向上测试,评分标准规定,做6个以上![]() 含6个
含6个![]() 为合格,做9个以上
为合格,做9个以上![]() 含9个
含9个![]() 为优秀,两组同学的测试成绩如下表:
为优秀,两组同学的测试成绩如下表:
成绩 | 4 | 5 | 6 | 7 | 8 | 9 |
甲组 | 1 | 2 | 5 | 2 | 1 | 4 |
乙组 | 1 | 1 | 4 | 5 | 2 | 2 |
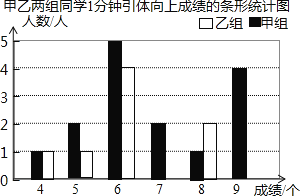
现将两组同学的测试成绩绘制成如下不完整的统计图表:
统计量 | 平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 |
甲组 | a | 6 | 6 |
|
|
|
乙组 |
| b | 7 |
|
|
|
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 统计表中的
统计表中的![]() ______,
______,![]() ______;
______;
![]() 人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.
人说甲组的优秀率高于乙组优秀率,所以甲组成绩比乙组成绩好,但也有人说乙组成绩比甲组成绩好,请你给出两条支持乙组成绩好的理由.