题目内容
【题目】如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE= °
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).

【答案】(1)90;(2)作图见解析,P(7,7),PH是分割线.
【解析】
试题(1)根据勾股定理求出△FEG的三边长,根据勾股定理逆定理可判定△FEG是直角三角形,且∠FGE="90" °.
(2)一方面,由于∠FPE=90°,从而根据直径所对圆周角直角的性质,点P在以EF为直径的圆上;另一方面,由于四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形,从而OP是正方形的对角线,即点P在∠FOE的角平分线上,因此可得P(7,7),PH是分割线.
试题解析:(1)连接FE,
∵E(8,0),F(0 , 6),G(4,8),
∴根据勾股定理,得FG=![]() ,EG=
,EG=![]() ,FE=10.
,FE=10.
∵![]() ,即
,即![]() .
.
∴△FEG是直角三角形,且∠FGE=90 °.
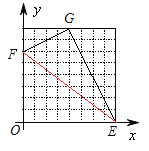
(2)作图如下:
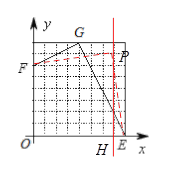
P(7,7),PH是分割线.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目