题目内容
【题目】正方形ABCD中,将一个直角三角板的直角顶点与点A重合,一条直角边与边BC交于点E(点E不与点B和点C重合),另一条直角边与边CD的延长线交于点F. 
(1)如图①,求证:AE=AF;
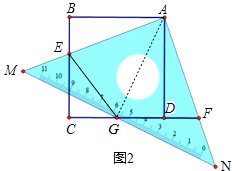
(2)如图②,此直角三角板有一个角是45°,它的斜边MN与边CD交于G,且点G是斜边MN的中点,连接EG,求证:EG=BE+DG;
(3)在(2)的条件下,如果 ![]() =
= ![]() ,那么点G是否一定是边CD的中点?请说明你的理由.
,那么点G是否一定是边CD的中点?请说明你的理由.
【答案】
(1)解:如图①,∵四边形ABCD是正方形,
∴∠B=∠BAD=∠ADC=∠C=90°,AB=AD.
∵∠EAF=90°,
∴∠EAF=∠BAD,
∴∠EAF﹣∠EAD=∠BAD﹣∠EAD,
∴∠BAE=∠DAF.
在△ABE和△ADF中
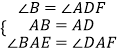 ,
,
∴△ABE≌△ADF(ASA)
∴AE=AF
(2)解:如图②,连接AG,
∵∠MAN=90°,∠M=45°,
∴∠N=∠M=45°,
∴AM=AN.
∵点G是斜边MN的中点,
∴∠EAG=∠NAG=45°.
∴∠EAB+∠DAG=45°.
∵△ABE≌△ADF,
∴∠BAE=∠DAF,AE=AF,
∴∠DAF+∠DAG=45°,
即∠GAF=45°,
∴∠EAG=∠FAG.
在△AGE和AGF中,
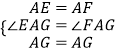 ,
,
∴△AGE≌AGF(SAS),
∴EG=GF.
∵GF=GD+DF,
∴GF=GD+BE,
∴EG=BE+DG
(3)解:G不一定是边CD的中点.
理由:设AB=6k,GF=5k,BE=x,
∴CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,
∴CG=CF﹣GF=k+x,
在Rt△ECG中,由勾股定理,得
(6k﹣x)2+(k+x)2=(5k)2,
解得:x1=2k,x2=3k,
∴CG=4k或3k.
∴点G不一定是边CD的中点.
【解析】(1)由正方形的性质可以得出∠B=∠BAD=∠ADC=∠C=90°,AB=AD,由直角三角形的性质∠EAF=∠BAD=90°,就可以得出∠BAE=∠DAF,证明△ABE≌△ADF就可以得出结论;(2)如图2,连结AG,由且点G是斜边MN的中点,△AMN是等腰直角三角形,就可以得出∠EAG=∠NAG=45°,就有∠EAB+∠DAG=45°,由△ABE≌△ADF可以得出∠BAE=∠DAF,AE=AF就可以得出△AGE≌AGF,从而得出结论;(3)设AB=6k,GF=5k,BE=x,就可以得出CE=6k﹣x,EG=5k,CF=CD+DF=6k+x,就有CG=CF﹣GF=k+x,由勾股定理就可以x的值而得出结论.
【考点精析】掌握正方形的性质是解答本题的根本,需要知道正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案