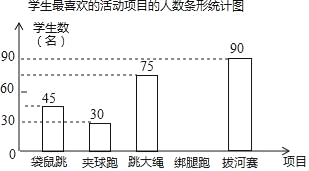
题目内容
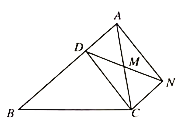
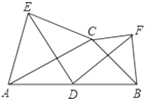
【题目】已知如图,D是△ABC中AB边上的中点,△ACE和△BCF分别是以AC、BC为斜边的等腰直角三角形,连接DE、DF.
求证:DE=DF.
【答案】证明见解析.
【解析】
分别取AC、BC中点M、N,连接MD、ND,再连接EM、FN,利用在直角三角形中:直角三角形斜边上的中线等于斜边的一半和已知条件证明四边形MDNC为平行四边形,再利用平行四边形的性质和已知条件证明△EMD≌△DNF即可.
证明:分别取AC、BC中点M、N,连接MD、ND,再连接EM、FN,
∵D为AB中点,∠AEC=90°,∠BFC=90°,
∴EM=![]() AC,FN=
AC,FN=![]() BC,
BC,
∵D是△ABC中AB边上的中点,
∴DN是△ABC的中位线.
∴DN=![]() AC,
AC,
∴EM=DN=![]() AC,FN=MD=
AC,FN=MD=![]() BC,
BC,
∵DN∥CM且DN=CM,
∴四边形MDNC为平行四边形,
∴∠CMD=∠CND.
∵∠EMC=∠FNC=90°,
∴∠EMC+∠CMD=∠FNC+∠CND,
即∠EMD=∠FND,
∴△EMD≌△DNF(SAS).
∴DE=DF.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目